题目内容
19.点A(1,1)在直线l:mx+ny=1上,则mn的最大值为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 由题意可得m+n=1,消去n由关于m的二次函数可得.
解答 解:∵点A(1,1)在直线l:mx+ny=1上,
∴m+n=1,∴mn=m(1-m)=-m2+m
由二次函数可知当m=-$\frac{1}{2×(-1)}$=$\frac{1}{2}$时,mn取最大值$\frac{1}{4}$.
故选:B.
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
7.已知正方体ABCD-A1B1C1D1的棱长为1,M为棱CC1的中点,则点M到平面A1BD的距离是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
14.若定义在R上的函数f(x),g(x)满足f(x-1)=f(1-x),g(x)=f(x-2),且f(x1)>f(x2)>f(1)(x1>x2>0),g(0)=3,g(2)=1,若g(x)在[0,m]上有最小值1,最大值3,则m的取值范围是( )
| A. | (0,+∞) | B. | (0,2] | C. | [2,4] | D. | [2,+∞) |
8.已知a,b∈R,且ab≠0,那么“a>b”是“lg(a-b)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
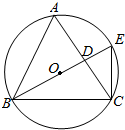 如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.
如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.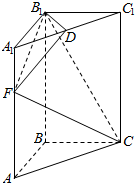 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.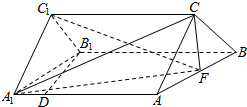 已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.
已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.