题目内容
已知函数f(x)=5-
,则f(x)在x∈(0,+∞)是 (增函数,减函数)若f(x)在[a,b](0<a<b)的值域是[a,b],则a= .
| 6 |
| x |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:①根据函数y=
的单调性,得出函数y=-
的单调性,即可得出函数f(x)=5-
的单调性;
②由函数f(x)在x∈(0,+∞)上的单调性,得出f(x)在[a,b]上的单调性,列出方程组,求出a的值.
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
②由函数f(x)在x∈(0,+∞)上的单调性,得出f(x)在[a,b]上的单调性,列出方程组,求出a的值.
解答:
解:①∵函数f(x)=5-
,
当x∈(0,+∞)时,y=
是减函数,
∴y=-
在x∈(0,+∞)上是增函数,
∴函数f(x)=5-
在x∈(0,+∞)上是增函数;
②∵函数f(x)=5-
在x∈(0,+∞)上是增函数,
且f(x)在[a,b](0<a<b)的值域是[a,b];
∴
,
即
,
解得a=2,b=3;
∴a的值是2.
故答案为:增函数;2.
| 6 |
| x |
当x∈(0,+∞)时,y=
| 6 |
| x |
∴y=-
| 6 |
| x |
∴函数f(x)=5-
| 6 |
| x |
②∵函数f(x)=5-
| 6 |
| x |
且f(x)在[a,b](0<a<b)的值域是[a,b];
∴
|
即
|
解得a=2,b=3;
∴a的值是2.
故答案为:增函数;2.
点评:本题考查了复合函数的单调性的判断问题,也考查了函数值域的应用问题,是综合性题目.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目

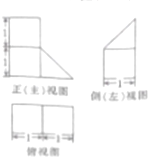 一个几何体按比列绘制的三视图如图所示(单位:m),则该几何体的体积为
一个几何体按比列绘制的三视图如图所示(单位:m),则该几何体的体积为