题目内容
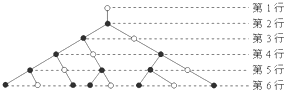
分形几何学是美籍法国数学家伯努瓦•B•曼德尔布罗特(Benoit B.Mandelbrot)在20世纪70年代创立的一门新学科,它的创立,为解决传统学科众多领域难题提供了全新的思路.如图是按照规则:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.所形成的一个树形图,则第11行的实心圆点的个数是 .

考点:归纳推理
专题:高考数学专题,推理和证明
分析:本题是一个探究型的题,可以看到第四行起每一行实心圆点的个数都是前两行实心圆点个数的和,由此可以得到一个递推关系,利用此递推关系求解即可.
解答:
解:由题意及图形知不妨构造这样一个数列{an}表示实心圆点的个数变化规律,令a1=1,a2=1,n≥3时,an=an-1+an-2,本数列中的n对应着图形中的第n+1行中实心圆点的个数.由此知a10即所求.
故各行中实心圆点的个数依次为1,1,2,3,5,8,13,21,34,55,…
a10=89,即第11行中实心圆点的个数是55.
故答案为:55.
故各行中实心圆点的个数依次为1,1,2,3,5,8,13,21,34,55,…
a10=89,即第11行中实心圆点的个数是55.
故答案为:55.
点评:本题考查数列的应用,是一个新定义的题,此类题关键是从定义中找出其规律来,构造出相应的数学模型,本题中所蕴含的规律是从第三项开始每一行中点数是前两项的点数的和,利用此规律求解

练习册系列答案
相关题目
已知a=
(
cosx-sinx)dx,则二项式(x2+
)5展开式中第三项的系数为( )
| ∫ | π 0 |
| 3 |
| a |
| x |
| A、80 | B、-80 |
| C、-40 | D、40 |
已知非零向量
,
,
满足
+
+
=0,向量
与
的夹角为60°,且|
|=|
|=1,则向量
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| A、30° | B、60° |
| C、120° | D、150° |
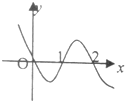
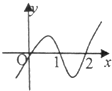
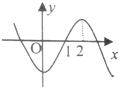
 函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )