题目内容
判断下列函数是否存在零点,如果存在,请求出:
(1)f(x)=-8x2+7x+1;(2)f(x)=x2+x+2;
(3)f(x)=x3+1.
(1)因为f(x)=-8x2+7x+1
=-(8x+1)(x-1),
令f(x)=0,可解得x=- 或x=1,
或x=1,
所以函数的零点为- 和1.
和1.
(2)令x2+x+2=0,因为Δ=12-4×1×2=-7<0,所以方程无实数解.
所以f(x)=x2+x+2不存在零点.
(3)因为f(x)=x3+1=(x+1)(x2-x+1),
令(x+1)(x2-x+1)=0,
解得x=-1.所以函数的零点为-1.

练习册系列答案
相关题目
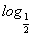 (x2-ax+3a)在区间[2,+∞)上是减函数,则实数a的取值范围是( )
(x2-ax+3a)在区间[2,+∞)上是减函数,则实数a的取值范围是( )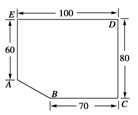
 ,cosx-cosy=
,cosx-cosy=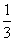 D.
D.
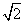 n mile的D处;乙船位于灯塔B的北偏西60°方向,与B相距5n mile的C处,则两艘轮船之间的距离为( )
n mile的D处;乙船位于灯塔B的北偏西60°方向,与B相距5n mile的C处,则两艘轮船之间的距离为( )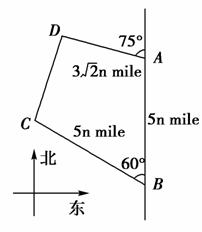
 n mile
n mile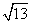 n mile D.3
n mile D.3