题目内容
已知y＝f(x)是定义在R上的奇函数，且x＜0时，f(x)＝1＋2x.
(1)求函数f(x)的解析式；
(2)画出函数f(x)的图象；
(3)写出函数f(x)单调区间及值域．
[解析] (1)因为y＝f(x)是定义在R上的奇函数，
所以f(0)＝－f(0)，所以f(0)＝0，
因为x＜0时，f(x)＝1＋2x，
所以x＞0时，f(x)＝－f(－x)＝－(1＋2－x)＝－1－
，
所以f(x)＝
(2)函数f(x)的图象为
(3)根据f(x)的图象知：
f(x)的单调增区间为(－∞，0)，(0，＋∞)；
值域为{y|1＜y＜2或－2＜y＜－1或y＝0}．
练习册系列答案
相关题目
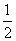，如果第一次未击中，则猎人进行第二次射击，但距离已是150 m，如果又未击中，则猎人进行第三次射击，但距离已是200 m，已知此猎人命中的概率与距离的平方成反比，求射击不超过三次击中野兔的概率．
是R上的单调递增函数，则实数a的取值范围是( )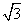
，f(2)＝－5，f(
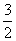)＝9，则下列结论正确的是( )