题目内容
已知f(x)=sin2x+sinxcosx,x∈[0,
]
(1)求f(x)的值域;
(2)若f(α)=
,求sin2α的值.
| π |
| 2 |
(1)求f(x)的值域;
(2)若f(α)=
| 5 |
| 6 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)首先,化简函数解析式:f(x)=
sin(2x-
)+
,然后,根据x∈[0,
],求解f(x)的值域;
(2)根据(1)的函数解析式,因为sin2α=sin(2α-
+
),先求解cos(2α-
)=
,然后求解.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
(2)根据(1)的函数解析式,因为sin2α=sin(2α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 3 |
解答:
解:(1)f(x)=sin2x+sinxcosx
=
+
=
sin(2x-
)+
∴f(x)=
sin(2x-
)+
.
∵x∈[0,
],
∴2x-
∈[-
,
],
当2x-
=-
,即x=0时,f(x)有最小值0.当2x-
=
时,f(x)有最大值
.
f(x)值域:[0,
].
(2)f(α)=
sin(2α-
)+
=
,得
sin(2α-
)=
,
∵α∈[0,
],
∴2α-
∈[-
,
],
又∵0<sin(2α-
)=
<
,
∴2α-
∈(0,
),
得cos(2α-
)=
=
,
∴sin2α=sin(2α-
+
)
=
[sin(2α-
)+cos(2α-
)]
=
.
∴sin2α的值
.
=
| 1-cos2x |
| 2 |
| sin2x |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴f(x)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∵x∈[0,
| π |
| 2 |
∴2x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
当2x-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
f(x)值域:[0,
| ||
| 2 |
(2)f(α)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 5 |
| 6 |
sin(2α-
| π |
| 4 |
| ||
| 3 |
∵α∈[0,
| π |
| 2 |
∴2α-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
又∵0<sin(2α-
| π |
| 4 |
| ||
| 3 |
| ||
| 2 |
∴2α-
| π |
| 4 |
| π |
| 4 |
得cos(2α-
| π |
| 4 |
1-(
|
| ||
| 3 |
∴sin2α=sin(2α-
| π |
| 4 |
| π |
| 4 |
=
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
=
2+
| ||
| 6 |
∴sin2α的值
2+
| ||
| 6 |
点评:本题重点考查了三角恒等变换公式、辅助角公式、二倍角公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
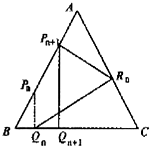 已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).
已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).