题目内容
不等式x2-kx+2>0恒成立,则实数k的取值范围是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:不等式x2-kx+2>0恒成立,则函数y=x2-kx+2的图象都在x轴的上方,得到判别式小于0.
解答:
解:因为不等式x2-kx+2>0恒成立,则函数y=x2-kx+2的图象都在x轴的上方,
所以判别式△=k2-8<0,解得-2
<k<2
;
故答案为:-2
<k<2
.
所以判别式△=k2-8<0,解得-2
| 2 |
| 2 |
故答案为:-2
| 2 |
| 2 |
点评:本题考查了一元二次不等式恒成立问题求参数范围;关键是与二次函数结合,得到判别式与0的不等式.

练习册系列答案
相关题目
已知函数①y=3x;②y=lnx;③y=x-1;④y=x
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的对应顺序一致的是( )
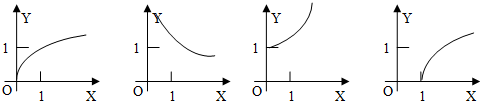
| 1 |
| 2 |
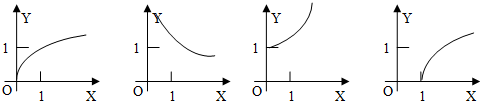
| A、④③①② | B、②③①④ |
| C、④①③② | D、②①③④ |
已知f(3x)=4xlog23,则f(4)的值等于( )
| A、4 | B、8 | C、16 | D、9 |
函数y=x
的图象是( )
| 3 |
| 2 |
A、 |
B、 |
C、 |
D、 |
设全集U=R,集合A={x|x≥1},B={x|0≤x<5},则集合(∁UA)∩B=( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|0≤x<1} |
| D、{x|0≤x≤1} |