题目内容
如图1,游乐场中的摩天轮匀速旋转,其最低点离地面5米,如果以你从最低点登上摩天轮的时刻开始计时,那么你与地面的距离y (m) 随时间x (min)变化的关系将如图所示(该图象近似于y=Asin(ωx+φ)+b(A>0,ω>0,-π≤φ≤0)的图象).
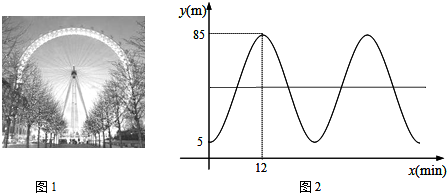
(Ⅰ)求出y(m)和x(min)的函数关系式;
(Ⅱ)当你第四次距离地面65米时与第一次距离地面65米时相隔多少时间?

(Ⅰ)求出y(m)和x(min)的函数关系式;
(Ⅱ)当你第四次距离地面65米时与第一次距离地面65米时相隔多少时间?
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)由图结合参数的意义可得A,b,ω,代点结合范围可得φ,可得解析式;
(Ⅱ)由题意可得cos
x=-
,可得第一次距离地面65米时的时间x1=8(min),第四次距离地面65米时的时间x4=40(min),作差可得答案.
(Ⅱ)由题意可得cos
| π |
| 12 |
| 1 |
| 2 |
解答:
解:(Ⅰ)由图可知,A=
=40,b=
=45,
又周期T=24,∴ω=
=
,
∴y=40sin(
x+φ)+45.
∵函数图象过点(0,5),
∴40sinφ+45=5,即sinφ=-1,
∵-π≤φ≤0,∴φ=-
.
∴y=40sin(
x-
)+45=45-40cos
x;
(Ⅱ)又y=45-40cos
x=65,可得cos
x=-
,
由图可知第一次距离地面65米时的时间x1∈(0,12)
∴
x1=
,x1=8(min).
∴由图象的对称性可知第二次距离地面65米时的时间x2=12+(12-x1)=12+4=16(min)
.∴第四次距离地面65米时的时间x4=x2+T=16+24=40(min).
∵x4-x1=40-8=32(min).
∴第四次距离地面65米时与第一次距离地面65米时相隔32min.
| 85-5 |
| 2 |
| 85+5 |
| 2 |
又周期T=24,∴ω=
| 2π |
| 24 |
| π |
| 12 |
∴y=40sin(
| π |
| 12 |
∵函数图象过点(0,5),
∴40sinφ+45=5,即sinφ=-1,
∵-π≤φ≤0,∴φ=-
| π |
| 2 |
∴y=40sin(
| π |
| 12 |
| π |
| 2 |
| π |
| 12 |
(Ⅱ)又y=45-40cos
| π |
| 12 |
| π |
| 12 |
| 1 |
| 2 |
由图可知第一次距离地面65米时的时间x1∈(0,12)
∴
| π |
| 12 |
| 2π |
| 3 |
∴由图象的对称性可知第二次距离地面65米时的时间x2=12+(12-x1)=12+4=16(min)
.∴第四次距离地面65米时的时间x4=x2+T=16+24=40(min).
∵x4-x1=40-8=32(min).
∴第四次距离地面65米时与第一次距离地面65米时相隔32min.
点评:本题考查是三角函数的图象和性质,涉及实际应用,属中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
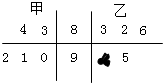 如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )
如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 从全校参加期末考试的试卷中,抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图,如图所示.图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最右边的一组频数是5.
从全校参加期末考试的试卷中,抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图,如图所示.图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最右边的一组频数是5.