题目内容
数列{an}满足a1=1,a2=2,an+1=2an+1(n≥2),则a21=( )
| A、3•220-1 |
| B、3•219-1 |
| C、219-1 |
| D、220-1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知的数列递推式构造出等比数列{an+1},由等比数列的通项公式求得a21.
解答:
解:由an+1=2an+1,得an+1+1=2(an+1)(n≥2),
∴
=2(n≥2),
∵
=
≠2,
∴数列{an+1}自第二项起构成以a2+1=3为首项,以2为公比的等比数列,
则a21+1=(a2+1)•219=3•219,
∴a21=3•219-1.
故选:B.
∴
| an+1+1 |
| an+1 |
∵
| a2+1 |
| a1+1 |
| 3 |
| 2 |
∴数列{an+1}自第二项起构成以a2+1=3为首项,以2为公比的等比数列,
则a21+1=(a2+1)•219=3•219,
∴a21=3•219-1.
故选:B.
点评:本题考查了数列递推式,考查了构造等比数列求数列的通项公式,是中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积胃( )
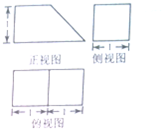

A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |
矩形ABCD满足AB=2,AD=1,点A、B分别在射线OM,ON上,∠MON为直角,当C到点O的距离最大时,∠BAO的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图为一三角形数阵,它满足:第n行首尾两数均为n,除去首尾的数为其肩上两数之和.如16=5+11,则第n行(n≥2)第2个数是
如图为一三角形数阵,它满足:第n行首尾两数均为n,除去首尾的数为其肩上两数之和.如16=5+11,则第n行(n≥2)第2个数是