题目内容
计算:
(1)1.1lg1+
-0.5-2+lg25+2lg2;
(2)sin2(-420°)+cos230°-sin(-210°)cos840°.
(1)1.1lg1+
| 3 | 64 |
(2)sin2(-420°)+cos230°-sin(-210°)cos840°.
考点:同角三角函数基本关系的运用,有理数指数幂的化简求值
专题:计算题
分析:(1)运用lg1=0,lg5+lg2=1以及根式的化简解之;
(2)利用三角函数的诱导公式化简.
(2)利用三角函数的诱导公式化简.
解答:
解:(1)1.1lg1+
-0.5-2+lg25+2lg2
=1.10+
-22+2lg5+2lg2
=1+4-4+2
=3.
(2)sin2(-420°)+cos230°-sin(-210°)cos840°
=sin2(360°+60°)+cos230°+sin(180°+30°)cos(720°+120°)
=sin260°+cos230°-sin30°cos120°
=
+
+
×
=
.
| 3 | 64 |
=1.10+
| 3 | 43 |
=1+4-4+2
=3.
(2)sin2(-420°)+cos230°-sin(-210°)cos840°
=sin2(360°+60°)+cos230°+sin(180°+30°)cos(720°+120°)
=sin260°+cos230°-sin30°cos120°
=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
点评:本题考查了代数式的化简以及三角函数式的化简与求值,用到了lg2+lg5=1,三角函数的诱导公式.

练习册系列答案
相关题目
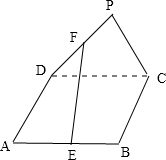 如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.
如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.