题目内容
求下列函数的导数:
(1)y=x-sin
•cos
;
(2)f(x)=
.
(1)y=x-sin
| x |
| 2 |
| x |
| 2 |
(2)f(x)=
| lnx+2x |
| x2 |
考点:导数的运算
专题:导数的综合应用
分析:直接利用导数的运算法则与基本初等函数的等式公式求解(1)(2).
解答:
解:(1)由y=x-sin
•cos
=x-
sinx,得
y′=(x-
sinx)′=1-
cosx;
(2)由f(x)=
,得
f′(x)=
=
=
.
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
y′=(x-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由f(x)=
| lnx+2x |
| x2 |
f′(x)=
| (lnx+2x)′•x2-(lnx+2x)•(x2)′ |
| x4 |
=
(
| ||
| x4 |
=
| x+2x•x2-2xlnx-2x•2x |
| x4 |
点评:本题考查了导数的运算法则,考查了基本初等函数的导数公式,是基础题.

练习册系列答案
相关题目
计算-3-2的结果是( )
| A、-9 | ||
| B、6 | ||
C、-
| ||
D、
|
命题“存在x0∈R,ex0≤0”的否定是( )
| A、不存在x0∈R,ex0>0 |
| B、存在x0∈R,ex0≥0 |
| C、对任意的x∈R,ex>0 |
| D、对任意的x∈R,ex≤0 |
已知圆柱的侧面展开图是边长分别为2a,a的矩形,则该圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
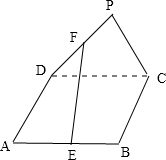 如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.
如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.