题目内容
已知α∈（-
，0），且sinα=-
，则cos（π+α）= ．
| π |
| 2 |
| 4 |
| 5 |
考点：同角三角函数基本关系的运用,运用诱导公式化简求值
专题：三角函数的求值
分析：由α的范围及sinα的值，利用同角三角函数间的基本关系求出cosα的值，原式利用诱导公式化简后把cosα的值代入计算即可求出值．
解答：
解：∵α∈（-
，0），且sinα=-
，
∴cosα=
=
，
则cos（π+α）=-cosα=-
．
故答案为：-
．
| π |
| 2 |
| 4 |
| 5 |
∴cosα=
| 1-sin2α |
| 3 |
| 5 |
则cos（π+α）=-cosα=-
| 3 |
| 5 |
故答案为：-
| 3 |
| 5 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
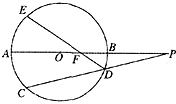已知⊙O的半径R=2，P为直径AB延长线上一点，PB=3，割线PDC交⊙O于D，C两点，E为⊙O上一点，且
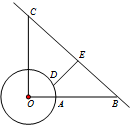为了适应市场需要，某地准备建一个圆形生猪储备基地（如图），它的附近有一条公路，从基地中心O处向东走1km是储备基地的边界上的点A，接着向东再走7km到达公路上的点B；从基地中心O向正北走8km到达公路的另一点C．现准备在储备基地的边界上选一点D，修建一条由D通往公路BC的专用线DE，则DE的最短距离为