题目内容
集合A={x|-3<x≤5},B={x|a+1≤x<4a+1},若B⊆A,则实数a的取值范围是 .
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:由B⊆A讨论B是否是空集.
解答:
解:①若B=∅,
则a+1≥4a+1,
解得,a≤0,符合B⊆A;
②若B≠∅,
则-3<a+1<4a+1≤5,
解得,0<a≤1,
综上所述,实数a的取值范围是:{a|a≤1}.
故答案为:{a|a≤1}.
则a+1≥4a+1,
解得,a≤0,符合B⊆A;
②若B≠∅,
则-3<a+1<4a+1≤5,
解得,0<a≤1,
综上所述,实数a的取值范围是:{a|a≤1}.
故答案为:{a|a≤1}.
点评:本题考查了集合包含关系的应用,注意分类讨论,属于基础题.

练习册系列答案
相关题目
数列{an}是等差数列,若
<-1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
| a11 |
| a10 |
| A、11 | B、17 | C、19 | D、21 |
一个凸多边形的内角成等差数列,其中最小的内角为
,公差为
,则这个多边形的边数为( )
| 2π |
| 3 |
| π |
| 36 |
| A、8 | B、9 | C、16 | D、9或16 |
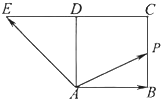 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中