题目内容
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量
=(1,2),
=(cos2A,cos2
),且
•
=1.
(1)求角A的大小;
(2)若b+c=2a=2
,求证:△ABC为等边三角形.
| m |
| n |
| A |
| 2 |
| m |
| n |
(1)求角A的大小;
(2)若b+c=2a=2
| 3 |
考点:正弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)利用向量的坐标和向量的数量积的运算求得关于cosA的一元二次方程求得cosA的值,则A可求得.
(2)根据已知条件利用余弦定理可求得a的值,b和c的关系,代入原式可求得b和c,进而判断出a=b=c,即三角形为等边三角形.
(2)根据已知条件利用余弦定理可求得a的值,b和c的关系,代入原式可求得b和c,进而判断出a=b=c,即三角形为等边三角形.
解答:
解:(1)由
=(1,2),
=(cos2A,cos2
),
得
•
=cos2A+2cos2
=2cos2A-1+cosA+1=2cos2A+cosA,
又因为
•
=1,
所以,2cos2A+cosA=1,解得cosA=
或cosA=-1,
因为0<A<π,
所以A=
,
(2)在△ABC中,a2=b2+c2-2bccosA且a=
所以,(
)2=b2+c2-2bc•
=b2+c2-bc①,
又b+c=2
,
∴b=2
-c,
代入①整理得c2-2
c+3=0,解得c=
,
∴b=
,
于是a=b=c=
,
即△ABC为等边三角形.
| m |
| n |
| A |
| 2 |
得
| m |
| n |
| A |
| 2 |
又因为
| m |
| n |
所以,2cos2A+cosA=1,解得cosA=
| 1 |
| 2 |
因为0<A<π,
所以A=
| π |
| 3 |
(2)在△ABC中,a2=b2+c2-2bccosA且a=
| 3 |
所以,(
| 3 |
| 1 |
| 2 |
又b+c=2
| 3 |
∴b=2
| 3 |
代入①整理得c2-2
| 3 |
| 3 |
∴b=
| 3 |
于是a=b=c=
| 3 |
即△ABC为等边三角形.
点评:本题主要考查了三角函数恒等变换的应用,余弦定理的应用.作为解三角形重要定理,应该熟练记忆余弦定理及其变形公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,a8-
a11=6,则数列{an}前9项和S9等于( )
| 1 |
| 2 |
| A、108 | B、72 | C、48 | D、24 |
 已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
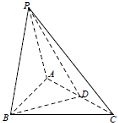 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.