题目内容
已知数列{an}的前n项和Sn=10n-n2,数列{bn}的每一项都有bn=|an|,求数列{bn}的前10项和.
考点:数列的求和,等差数列的前n项和
专题:等差数列与等比数列
分析:根据题意可得{bn}是由一个首项为正数,公差为负数的等差数列,{an}的各项取绝对值后得到一个新数列,因此求{bn}的前10项和可转化为求数列{an}的和.
解答:
解:∵Sn=10n-n2,
∴Sn-1=10(n-1)-(n-1)2,(n≥2)
两式相减可得an=11-2n
∵n=1时,a1=S1=10-1=9,满足上式
∴an=11-2n,∴bn=|11-2n|.
显然n≤5时,bn=an=11-2n,Tn=10n-n2.
n≥6时,bn=-an=2n-11,
∴Tn=(a1+a2+…+a5)-(a6+a7+…+an)=2S5-Sn=50-10n+n2
故Tn=
数列{bn}的前10项和为:
T10=102-10×10+50=50.
∴Sn-1=10(n-1)-(n-1)2,(n≥2)
两式相减可得an=11-2n
∵n=1时,a1=S1=10-1=9,满足上式
∴an=11-2n,∴bn=|11-2n|.
显然n≤5时,bn=an=11-2n,Tn=10n-n2.
n≥6时,bn=-an=2n-11,
∴Tn=(a1+a2+…+a5)-(a6+a7+…+an)=2S5-Sn=50-10n+n2
故Tn=
|
数列{bn}的前10项和为:
T10=102-10×10+50=50.
点评:本题主要考查了数列的通项与求和方法的运用,考查学生的分析能力,属于中档题.

练习册系列答案
相关题目
在平面直角坐标系中,以点(1,1)为圆心,以
为半径的圆在以直角坐标系的原点为极点,以ox轴为极轴的极坐标系中对应的极坐标方程为( )
| 2 |
A、ρ=2
| ||||
B、ρ=2
| ||||
C、ρ=2
| ||||
D、ρ=2
|
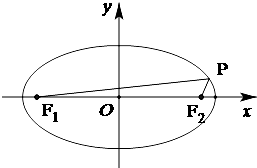 已知椭圆
已知椭圆