题目内容
在等差数列{an}中，a8-
a11=6，则数列{an}前9项和S9等于（ ）
| 1 |
| 2 |
| A、108 | B、72 | C、48 | D、24 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设等差数列{an}的公差为d，代入已知可得a5=12，而由求和公式和性质可得S9=9a5，代入计算可得．
解答：
解：设等差数列{an}的公差为d，
代入a8-
a11=6可得a1+7d-
（a1+10d）=6，
化简可得a1+4d=12，即a5=12，
故S9=9a5=108，
故选：A．
代入a8-
| 1 |
| 2 |
| 1 |
| 2 |
化简可得a1+4d=12，即a5=12，
故S9=9a5=108，
故选：A．
点评：本题考查等差数列的前n项和公式，涉及等差数列的性质，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知，如图，在梯形ABCD中，AD∥BC，AD=3，BC=7，点M，N分别是对角线BD，AC的中点，则MN=（ ）| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
对于实数x，“x＞6”是“x＞10”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在平面直角坐标系中，以点（1，1）为圆心，以
为半径的圆在以直角坐标系的原点为极点，以ox轴为极轴的极坐标系中对应的极坐标方程为（ ）
| 2 |
A、ρ=2
| ||||
B、ρ=2
| ||||
C、ρ=2
| ||||
D、ρ=2
|
定义一种新运算：a?b=
，已知函数f（x）=（1+
）?3log2（x+1），若方程f（x）-k=0恰有两个不相等的实根，则实数k的取值范围为（ ）
|
| 2 |
| x |
| A、（-∞，3） |
| B、（1，3） |
| C、（-∞，-3）∪（1，3） |
| D、（-∞，-3）∪（0，3） |
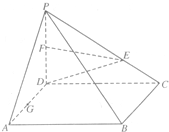如图，ABCD是正方形，PD⊥底面ABCD，点E在PC上，F，G分别是PD和AD的中点．
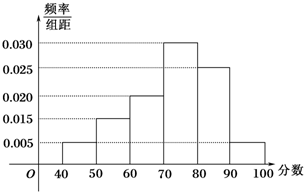从参加高一年级某次模块考试中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
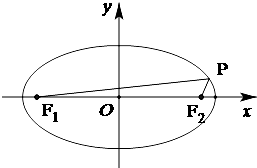已知椭圆