题目内容
已知命题p:“直线x+y-a=0与圆(x-1)2+y2=1有公共点”,命题q:函数f(x)=ax2+ax+1没有零点,若命题p∧q为假命题,p∨q为真命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:当p为真命题时,联立
,则2x2-2(a+1)x+a2=0有实数根,可得△≥0,解出即可;当q为真命题时,分类讨论:当a=0时,方程无实根符合题意;当a≠0时,△<0解得a的取值范围.由命题p∧q为假命题,p∨q为真命题可知,命题p与命题q有且只有一个为真.即可得出.
|
解答:
解:当p为真命题时
由
,则2x2-2(a+1)x+a2=0,
∴△=4(a+1)2-8a2≥0
∴1-
≤a≤1+
.
当q为真命题时,
①当a=0时,方程无实根符合题意;
②当a≠0时,△=a2-4a<0解得0<a<4,
∴0≤a<4.
由命题p∧q为假命题,p∨q为真命题可知,命题p与命题q有且只有一个为真.
当p真q假时,
,∴1-
≤a<0;
当p假q真时
,∴1+
<a<4.
综合得:1-
≤a<0或1+
<a<4.
由
|
∴△=4(a+1)2-8a2≥0
∴1-
| 2 |
| 2 |
当q为真命题时,
①当a=0时,方程无实根符合题意;
②当a≠0时,△=a2-4a<0解得0<a<4,
∴0≤a<4.
由命题p∧q为假命题,p∨q为真命题可知,命题p与命题q有且只有一个为真.
当p真q假时,
|
| 2 |
当p假q真时
|
| 2 |
综合得:1-
| 2 |
| 2 |
点评:本题考查了直线与圆的位置关系、函数的零点、复合命题真假的判定,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
对于实数x,“x>6”是“x>10”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
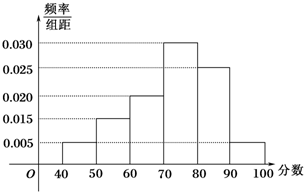 从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.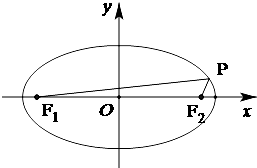 已知椭圆
已知椭圆 如图,正方体ABCD-A1B1C1D1的棱长是2,点E、F分别是两条棱的中点
如图,正方体ABCD-A1B1C1D1的棱长是2,点E、F分别是两条棱的中点