题目内容
设平面向量
=(-2,1),
=(λ,-1),若
与
的夹角是钝角,则λ的范围是 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:由于
与
的夹角是钝角,可得
•
=-2λ-1<0,且
•
≠-|
| |
|.解出即可.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:∵
与
的夹角是钝角,
∴
•
=-2λ-1<0,且
•
≠-|
| |
|.
解得λ>-
,且λ≠2.
故答案为:(-
,2)∪(2,+∞)
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
解得λ>-
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
点评:本题考查了向量的夹角公式,属于基础题.

练习册系列答案
相关题目
以(-1,2)为圆心,
为半径的圆的方程为( )
| 5 |
| A、x2+y2-2x+4y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2+2x-4y=0 |
| D、x2+y2-2x-4y=0 |
下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数为( )
| A、f(x)=x-1 | ||
| B、f(x)=cosx | ||
| C、f(x)=2|x| | ||
D、f(x)=log
|
若(
)x-1>9,则x的取值范围是( )
| 1 |
| 3 |
| A、(-1,+∞) |
| B、(-∞,2) |
| C、(-∞,-1) |
| D、[2,+∞) |
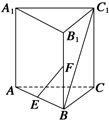 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是