题目内容
18．
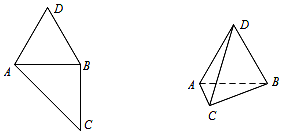如图，四边形ABCD中，△ABD是正三角形，△ABC是等腰直角三角形，∠ABC=90°，沿AB将△ABD折起，使得平面ABD⊥平面ABC，若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$，则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$．
分析 由题意，三棱锥D-ABC的外接球的半径为$\sqrt{\frac{7}{3}}$，再求出AB，即可求出三棱锥D-ABC的侧面ACD的面积
解答 解：由题意，三棱锥D-ABC的外接球的半径为$\sqrt{\frac{7}{3}}$，
设AB=4a，球心到平面ABC的距离为h，则由勾股定理可得$\frac{7}{3}$=h2+8a2=$4{a}^{2}+（2\sqrt{3}a-h）^{2}$，∴a=$\frac{1}{2}$．
△ACD中，AD=4a，AC=DC=4$\sqrt{2}a$，∴三棱锥D-ABC的侧面ACD的面积为$\frac{1}{2}•4a•\sqrt{32{a}^{2}-4{a}^{2}}$=$\sqrt{7}$，
故答案为$\sqrt{7}$．
点评 本题考查三棱锥D-ABC的外接球的表面积，考查勾股定理的运用，属于中档题．
练习册系列答案
相关题目
9．函数$f（x）=Asin（ωx+\frac{π}{4}）（ω＞0）$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{4}$个单位 | D． | 向右平移$\frac{3π}{4}$个单位 |
6．某兴趣小组有男生20人，女生10人，从中抽取一个容量为5的样本，恰好抽到2名男生和3名女生，则
①该抽样可能是系统抽样；
②该抽样可能是随机抽样：
③该抽样一定不是分层抽样；
④本次抽样中每个人被抽到的概率都是$\frac{1}{5}$．
其中说法正确的为（ ）
①该抽样可能是系统抽样；
②该抽样可能是随机抽样：
③该抽样一定不是分层抽样；
④本次抽样中每个人被抽到的概率都是$\frac{1}{5}$．
其中说法正确的为（ ）
| A． | ①②③ | B． | ②③ | C． | ②③④ | D． | ③④ |
3．已知双曲线C的中心在原点，焦点在y轴上，若双曲线C的一条渐近线与直线$\sqrt{3}x+y-4=0$平行，则双曲线C的离心率为（ ）
| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
10．已知α为第二象限角，sin（π+α）=-$\frac{1}{3}$，则tanα=（ ）
| A． | -$\frac{\sqrt{2}}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
7．在直三棱柱ABC-A1B1C1中，AA1=AB=BC=2，$∠ABC=\frac{π}{2}$，E，F分别为棱AB，AC的中点，则直线A1E和C1F的夹角余弦值为（ ）
| A． | $\frac{{\sqrt{30}}}{10}$ | B． | $\frac{{\sqrt{30}}}{6}$ | C． | $\frac{{\sqrt{10}}}{6}$ | D． | $\frac{{2\sqrt{30}}}{15}$ |