题目内容
2．如图是某几何体的三视图，则该几何体的体积为（ ）
| A． | 6 | B． | 9 | C． | 12 | D． | 18 |
分析 由已知中的三视图可得：该几何体是两个三棱柱形成的组合体，进而可得答案．
解答 解：由已知中的三视图可得：该几何体是两个三棱柱形成的组合体，
下部的三棱柱，底面面积为：$\frac{1}{2}$×4×3=6，高为1，体积为：6；
上部的三棱柱，底面面积为：$\frac{1}{2}$×2×3=3，高为1，体积为：3；
故组合体的体积V=6+3=9，
故选：B
点评 本题考查的知识点是棱柱的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．已知α为第二象限角，sin（π+α）=-$\frac{1}{3}$，则tanα=（ ）
| A． | -$\frac{\sqrt{2}}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
17．
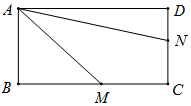如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）
如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{5π}{12}$ |
7．在直三棱柱ABC-A1B1C1中，AA1=AB=BC=2，$∠ABC=\frac{π}{2}$，E，F分别为棱AB，AC的中点，则直线A1E和C1F的夹角余弦值为（ ）
| A． | $\frac{{\sqrt{30}}}{10}$ | B． | $\frac{{\sqrt{30}}}{6}$ | C． | $\frac{{\sqrt{10}}}{6}$ | D． | $\frac{{2\sqrt{30}}}{15}$ |
14．已知函数$f（x）=\sqrt{x}sinx$，则f'（π）=（ ）
| A． | $\sqrt{π}$ | B． | $\frac{{\sqrt{π}}}{2π}$ | C． | $-\sqrt{π}$ | D． | $\frac{{\sqrt{2π}}}{2π}$ |