题目内容
8.${({2\frac{7}{9}})^{0.5}}+{0.1^{-2}}+{({2\frac{10}{27}})^{-\frac{2}{3}}}-{π^0}+\frac{37}{48}$=$\frac{807}{8}$.分析 利用有理数指数幂的性质、运算法则求解.
解答 解:${({2\frac{7}{9}})^{0.5}}+{0.1^{-2}}+{({2\frac{10}{27}})^{-\frac{2}{3}}}-{π^0}+\frac{37}{48}$
=($\frac{25}{9}$)${\;}^{\frac{1}{2}}$+(10-1)-2+[($\frac{4}{3}$)3]${\;}^{-\frac{2}{3}}$-1+$\frac{37}{48}$
=$\frac{5}{3}+100$-$\frac{9}{16}$-1+$\frac{37}{48}$
=$\frac{807}{8}$.
故答案为:$\frac{807}{8}$.
点评 本题考查有理数指数幂化简求值,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.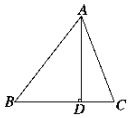 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件:
(1)∠B+∠DAC=90°;
(2)∠B=∠DAC;
(3)$\frac{CD}{AD}$=$\frac{AC}{AB}$;
(4)AB2=BD•BC.
其中一定能够判定△ABC是直角三角形的共有( )
 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件:(1)∠B+∠DAC=90°;
(2)∠B=∠DAC;
(3)$\frac{CD}{AD}$=$\frac{AC}{AB}$;
(4)AB2=BD•BC.
其中一定能够判定△ABC是直角三角形的共有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
16.设实数x,y满足约束条件$\left\{\begin{array}{l}y≥1\\ y≤2x-1\\ x+y≤m\end{array}\right.$且目标函数z=x-y的最小值为-1,则m=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
20.函数f(x)=ax3+bx2+cx+d(a≠0)在(-∞,+∞)上是减少的,则下列各式中成立的是( )
| A. | a>0,b2+3ac≥0 | B. | a>0,b2-3ac≤0 | C. | a<0,b2+3ac≥0 | D. | a<0,b2-3ac≤0 |
17.已知a,b∈R,i是虚数单位,若a+i=2-bi,则(a+bi)2=( )
| A. | 3-4i | B. | 3+4i | C. | 4-3i | D. | 4+3i |
18.下列函数中,周期为π的奇函数是( )
| A. | y=sin2x | B. | y=tan2x | C. | y=sin2x+cos2x | D. | y=sinxcosx |