题目内容
18．下列函数中，周期为π的奇函数是（ ）| A． | y=sin2x | B． | y=tan2x | C． | y=sin2x+cos2x | D． | y=sinxcosx |
分析 根据题意，依次分析选项，求出函数的周期与奇偶性，分析即可得答案．
解答 解：根据题意，依次分析选项：
对于A、y=sin2x=$\frac{1-cos2x}{2}$，为偶函数，周期为$\frac{2π}{2}$=π，不符合题意；
对于B、y=tan2x，为奇函数，其周期为$\frac{π}{2}$，不符合题意；
对于C、y=sin2x+cos2x=$\sqrt{2}$sin（2x+$\frac{π}{4}$），为非奇非偶函数，不符合题意；
对于D、y=sinxcosx=$\frac{1}{2}$sin2x，为奇函数，且其周期为$\frac{2π}{2}$=π，符合题意；
故选：D．
点评 本题考查三角函数的周期的计算，关键是正确将三角函数化简变形．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
6．
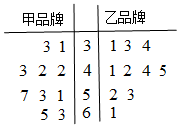某商场对甲、乙两种品牌的商品进行为期100天的营销活动，为调查这100天的日销售情况，随机抽取了10天的日销售量（单位：件）作为样本，样本数据的茎叶图如图．若日销量不低于50件，则称当日为“畅销日”．
（Ⅰ）现从甲品牌日销量大于40且小于60的样本中任取两天，求这两天都是“畅销日”的概率；
（Ⅱ）用抽取的样本估计这100天的销售情况，请完成这两种品牌100天销量的2×2列联表，并判断是否有99%的把握认为品牌与“畅销日”天数有关．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
某商场对甲、乙两种品牌的商品进行为期100天的营销活动，为调查这100天的日销售情况，随机抽取了10天的日销售量（单位：件）作为样本，样本数据的茎叶图如图．若日销量不低于50件，则称当日为“畅销日”．（Ⅰ）现从甲品牌日销量大于40且小于60的样本中任取两天，求这两天都是“畅销日”的概率；
（Ⅱ）用抽取的样本估计这100天的销售情况，请完成这两种品牌100天销量的2×2列联表，并判断是否有99%的把握认为品牌与“畅销日”天数有关．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
10．设α，β是一个钝角三角形的两个锐角，下列四个不等式中的正确的个数是（ ）
（1）cosα＞sinβ
（2）$sinα+sinβ＜\sqrt{2}$
（3）cosα+cosβ＞1
（4）$\frac{1}{2}tan（{α+β}）＜tan\frac{α+β}{2}$．
（1）cosα＞sinβ
（2）$sinα+sinβ＜\sqrt{2}$
（3）cosα+cosβ＞1
（4）$\frac{1}{2}tan（{α+β}）＜tan\frac{α+β}{2}$．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．已知直线$y=\frac{{2\sqrt{3}}}{3}x$和椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$交于不同的两点M，N，若M，N在x轴上的射影恰好为椭圆的两个焦点，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{3}$ |