题目内容
已知函数f(x)=ax3+bx2+cx(a,b,c∈R).
(Ⅰ)当a>0时,f(x)在x=1处有极大值2,试讨论f(x)在[0,2]上的单调性.
(Ⅱ)若f(x)为[-2,2]上的奇函数,且任意的x∈[-2,2]恒有|f(x)|≤2,求c的最大值.
(Ⅰ)当a>0时,f(x)在x=1处有极大值2,试讨论f(x)在[0,2]上的单调性.
(Ⅱ)若f(x)为[-2,2]上的奇函数,且任意的x∈[-2,2]恒有|f(x)|≤2,求c的最大值.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)先求出f′(x),根据条件f(x)在x=1处有极大值2,便可得到两个等式:f′(1)=0,f(1)=2.这样便得到关于a,b,c的两个等式,从而能够找到a,b,c的关系.告诉了a>0,所以可以选择用a来表示b,c.带入导函数,然后讨论a,判断导数符号,从而来讨论f(x)在[0,2]上的单调性.
(Ⅱ)根据f(x)为[-2,2]上的奇函数,便求出b=0,从而使得导函数中只含a,c.这时候,讨论a取值情况,拿a和0做比较即可.由于f(x)在[-2,2]为奇函数,所以使f(x)在[-2,2]恒有|f(x)|≤2成立,可变成在[0,2]上|f(x)|≤2即可,这样便简化解题过程.下面要做的是讨论函数f(x)在[0,2]上的单调性,根据单调性用a,c表示出f(x)的最大值或最小值,限制最大值小于等于2,最小值大于等于-2,从而得到关于a,c的不等式,从而求出c的最大值.
(Ⅱ)根据f(x)为[-2,2]上的奇函数,便求出b=0,从而使得导函数中只含a,c.这时候,讨论a取值情况,拿a和0做比较即可.由于f(x)在[-2,2]为奇函数,所以使f(x)在[-2,2]恒有|f(x)|≤2成立,可变成在[0,2]上|f(x)|≤2即可,这样便简化解题过程.下面要做的是讨论函数f(x)在[0,2]上的单调性,根据单调性用a,c表示出f(x)的最大值或最小值,限制最大值小于等于2,最小值大于等于-2,从而得到关于a,c的不等式,从而求出c的最大值.
解答:
解:(I)f′(x)=3ax2+2bx+c,由于f(x)在x=1处有极大值2,则
,即
,则c=a+4,b=-2-2a,从而f′(x)=3ax2+2bx+c=3a(x-1)(x-
).
由于f(x)在x=1处有极大值,且a>0,则
>1,即0<a<2.
(1)当
<2,即
<a<2时,x∈(0,1)时,f′(x)>0,∴f(x)在[0,1)上单调递增;
x∈(1,
)时,f′(x)<0,∴f(x)在[1,
)上单调递减;
x∈(
,2)时,f′(x)>0,∴f(x)在[
,2]上单调递增.
(2)当
≥2,即0<a≤
时,x∈(0,1)时,f′(x)>0,∴f(x)在[0,1]上单调递增;
x∈(1,2)时,f′(x)<0,∴f(x)在(1,2]上单调递减.
(II)由于f(x)为[-2,2]上的奇函数,从而b=0,从而f(x)=ax3+cx,
要使得任意的x∈[-2,2]恒有|f(x)|≤2,则只需任意的x∈[0,2]时|f(x)|≤2恒成立.
显然要使得c取最大值,则c>0.
(1)当a≥0时,则当x∈[0,2]时,f′(x)>0,故f(x)在[0,2]上单调递增.由于任意的x∈[0,2]恒有|f(x)|≤2,则只需f(2)=8a+2c≤2,从而c≤1-4a≤1,即c的最大可能值为1.
(2)当a<0时,则f′(x)=3ax2+c,令3ax2+c=0,x=±
.
i)当
≥2时,当x∈[0,2]时,恒有f′(x)≥0,故f(x)在[0,2]上单调递增.要使得任意的x∈[0,2]恒有|f(x)|≤2,则只需f(2)=8a+2c≤2,从而c≤1-4a.
考虑到
≥2,即-4a≤
,从而c≤1+
,故c≤
,即c的最大可能值为
.
ii)当0<
<2时,则当x∈[0,
]时,有f′(x)≥0;当x∈[
,2]时,有f'(x)≤0,从而f(x)在[0,
]上单调递增,在[
,2]上单调递减,故要使得任意的x∈[0,2]恒有|f(x)|≤2,则只需f(
)=
≤2,且f(2)=8a+2c≥-2
即c3≤-27a,且0<-a≤
,故c3≤
+
,即(c-3)(4c2+12c+9)=(c-3)(2c+3)2≤0
故c≤3,即c的最大可能值为3.
由上述可知,c的最大可能值为3.下面我们再证明c=3是可取的,令f(x)=-x3+3x,x∈[-2,2],则f′(x)=-3x2+3=-3(x-1)(x+1),则当f′(x)≥0时有-1≤x≤1,故f(x)在[-2,-1]单调递减,在[-1,1]上单调递增,在[1,2]上单调递减,故fmax=max{f(-2),f(1)}=max{2,2}=2,fmin=min{f(-1),f(2)}=min{-2,-2}=-2
从而任意的x∈[-2,2]恒有|f(x)|≤2成立.
综合上述,实数c的最大值为3.
|
|
| a+4 |
| 3a |
由于f(x)在x=1处有极大值,且a>0,则
| a+4 |
| 3a |
(1)当
| a+4 |
| 3a |
| 4 |
| 5 |
x∈(1,
| a+4 |
| 3a |
| a+4 |
| 3a |
x∈(
| a+4 |
| 3a |
| a+4 |
| 3a |
(2)当
| a+4 |
| 3a |
| 4 |
| 5 |
x∈(1,2)时,f′(x)<0,∴f(x)在(1,2]上单调递减.
(II)由于f(x)为[-2,2]上的奇函数,从而b=0,从而f(x)=ax3+cx,
要使得任意的x∈[-2,2]恒有|f(x)|≤2,则只需任意的x∈[0,2]时|f(x)|≤2恒成立.
显然要使得c取最大值,则c>0.
(1)当a≥0时,则当x∈[0,2]时,f′(x)>0,故f(x)在[0,2]上单调递增.由于任意的x∈[0,2]恒有|f(x)|≤2,则只需f(2)=8a+2c≤2,从而c≤1-4a≤1,即c的最大可能值为1.
(2)当a<0时,则f′(x)=3ax2+c,令3ax2+c=0,x=±
|
i)当
|
考虑到
|
| c |
| 3 |
| c |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
ii)当0<
|
|
|
|
|
|
| 2c |
| 3 |
|
即c3≤-27a,且0<-a≤
| 1+c |
| 4 |
| 1 |
| 4 |
| c |
| 4 |
故c≤3,即c的最大可能值为3.
由上述可知,c的最大可能值为3.下面我们再证明c=3是可取的,令f(x)=-x3+3x,x∈[-2,2],则f′(x)=-3x2+3=-3(x-1)(x+1),则当f′(x)≥0时有-1≤x≤1,故f(x)在[-2,-1]单调递减,在[-1,1]上单调递增,在[1,2]上单调递减,故fmax=max{f(-2),f(1)}=max{2,2}=2,fmin=min{f(-1),f(2)}=min{-2,-2}=-2
从而任意的x∈[-2,2]恒有|f(x)|≤2成立.
综合上述,实数c的最大值为3.
点评:考查的知识点有:利用导数讨论函数的单调性,利用导数求函数的极值,函数的奇偶性.要注意的是,根据函数在x=1处有极大值,变得到导函数的另一零点大于1.对于第二问,求c的最大值,先求关于a,c的不等式.根据函数是奇函数,对于函数在[-2,2]恒有|f(x)|≤2,只需满足在[0,2]有|f(x)|≤2即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=
如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=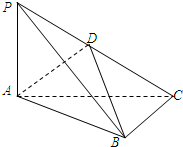 在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=
在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=