题目内容
对于函数f(x)=
(其中a为非零实数),给出以下命题:
①当a>0时,f(x)在定义域上为单调函数;
②当a=-1时,函数f(x)的图象的关于原点中心对称;
③对于任意的a∈R+,函数f(x)均能取到最小值为2
;
④对于任意的a∈R+,函数f(x)为偶函数;
⑤当a=1时,对于满足0<x1<x2<1的所有x1,x2,总有f(x2)-f(x1)<
ln2(x2-x1).
其中所有正确命题的序号为( )
| 22x+a |
| 2x |
①当a>0时,f(x)在定义域上为单调函数;
②当a=-1时,函数f(x)的图象的关于原点中心对称;
③对于任意的a∈R+,函数f(x)均能取到最小值为2
| a |
④对于任意的a∈R+,函数f(x)为偶函数;
⑤当a=1时,对于满足0<x1<x2<1的所有x1,x2,总有f(x2)-f(x1)<
| 3 |
| 2 |
其中所有正确命题的序号为( )
| A、①②③ | B、③④⑤ |
| C、②③ | D、②③⑤ |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用
分析:对于①,由复合函数的单调性加以判断;
对于②,取a=-1后,判断函数为奇函数,从而得到命题正确;
对于③,直接由①中得到的函数的单调性求得最小值,说明命题正确;
对于④,直接由函数奇偶性的定义说明真假;
对于⑤,求出函数的导函数,判断导函数的增减性,由割线的斜率小于函数在x=1处的切线的斜率说明命题正确.
对于②,取a=-1后,判断函数为奇函数,从而得到命题正确;
对于③,直接由①中得到的函数的单调性求得最小值,说明命题正确;
对于④,直接由函数奇偶性的定义说明真假;
对于⑤,求出函数的导函数,判断导函数的增减性,由割线的斜率小于函数在x=1处的切线的斜率说明命题正确.
解答:
解:对于①,令t=2x,f(t)=t+
,
外层函数f(t)=t+
在(0,
]单调递减,在[
,+∞)单调递增,内层函数t=2x为增函数,
∴①不正确;
对于②,当a=-1时,f(x)=2x-
.
∵f(-x)=2-x-
=
-2x=-f(x),
∴函数f(x)为奇函数,奇函数的图象关于原点对称,
∴②正确;
对于③,由①知:当t=
时,f(x)最小,最小值是2
,
由2x=
⇒x=
=
,
∴③正确;
对于④,∵当a=3时,f(x)=2x+
,
f(-x)=2-x+
=3•2x+
≠2x+
=f(x),函数不是偶函数,
∴④不正确;
对于⑤,当a=1时,f(x)=2x+
,
∵f′(x)=(2x-
)ln2为增函数,
∴对于满足0<x1<x2<1的所有x1,x2,
总有
<f′(x)max<f′(1)=
ln2.
即f(x2)-f(x1)<
ln2(x2-x1).
∴⑤正确.
综上,正确命题的序号是②③⑤.
故选:D.
| a |
| t |
外层函数f(t)=t+
| a |
| t |
| a |
| a |
∴①不正确;
对于②,当a=-1时,f(x)=2x-
| 1 |
| 2x |
∵f(-x)=2-x-
| 1 |
| 2-x |
| 1 |
| 2x |
∴函数f(x)为奇函数,奇函数的图象关于原点对称,
∴②正确;
对于③,由①知:当t=
| a |
| a |
由2x=
| a |
| log |
2 |
| 1 |
| 2 |
| log | a 2 |
∴③正确;
对于④,∵当a=3时,f(x)=2x+
| 3 |
| 2x |
f(-x)=2-x+
| 3 |
| 2-x |
| 1 |
| 2x |
| 3 |
| 2x |
∴④不正确;
对于⑤,当a=1时,f(x)=2x+
| 1 |
| 2x |
∵f′(x)=(2x-
| 1 |
| 2x |
∴对于满足0<x1<x2<1的所有x1,x2,
总有
| f(x2)-f(x1) |
| x2-x1 |
| 3 |
| 2 |
即f(x2)-f(x1)<
| 3 |
| 2 |
∴⑤正确.
综上,正确命题的序号是②③⑤.
故选:D.
点评:本题考查了命题的真假判断与应用,考查了函数的基本性质,是中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
按照如图的程序框图执行,若输出的X值为31,则M处的条件为( )


| A、k≤2 | B、k<3 |
| C、k≤3 | D、k≤4 |
如图所示的程序框图,如果输入m=225,n=135,那么输出的值为( )


| A、45 | B、5 | C、15 | D、90 |
在△ABC中,BC=
,AC=3,sinC=2sinA,则tan(A-
)的值为( )
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
| D、3 |
已知复数z1=2+i,z2=a-i,z1•z2是实数,则实数a=( )
| A、2 | B、3 | C、4 | D、5 |
已知某空间几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )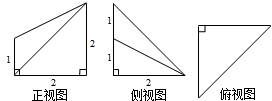

| A、2cm3 | ||
B、
| ||
| C、1cm3 | ||
| D、6cm3 |
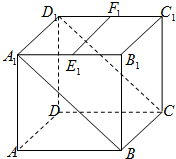 如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为
如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为