题目内容
已知函数 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(I)求曲线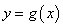 在点
在点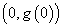 处的切线方程;
处的切线方程;
(II)若对任意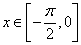 ,不等式
,不等式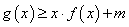 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(III)试探究当 时,方程
时,方程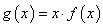 的解的个数,并说明理由.
的解的个数,并说明理由.
解:(Ⅰ)依题意得,
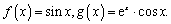
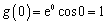 ,
,
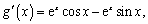
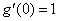 ,
,
所以曲线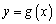 在点
在点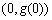 处的切线方程为
处的切线方程为
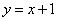 ………………………………………4分
………………………………………4分
(Ⅱ)等价于对任意 ,
,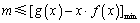 .
.
设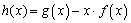 ,
, .
.
则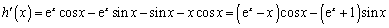
因为 ,所以
,所以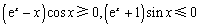 ,
,
所以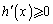 ,故
,故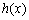 在
在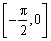 单调递增,
单调递增,
因此当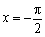 时,函数
时,函数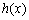 取得最小值
取得最小值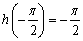 ;
;
所以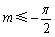 ,即实数
,即实数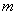 的取值范围是
的取值范围是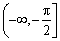 . ………………………………10分
. ………………………………10分
(Ⅲ)设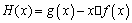 ,
,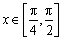 .
.
当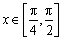 时,
时,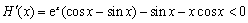 ,所以函数
,所以函数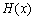 在
在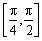 上单调递减,故函数
上单调递减,故函数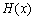 在
在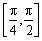 至多只有一个零点,
至多只有一个零点,
又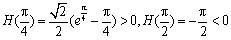 ,而且函数
,而且函数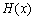 在
在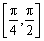 上是连续不断的,
上是连续不断的,
因此,函数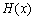 在
在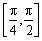 上有且只有一个零点.…………………………………13分
上有且只有一个零点.…………………………………13分

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 的体积为
的体积为 
 则满足
则满足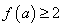 的实数a的取值范围是
的实数a的取值范围是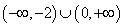 B.
B.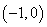
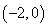 D.
D.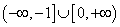

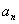 },
},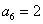 ,则此数列的前11项的和
,则此数列的前11项的和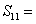
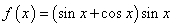 ,
,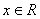 ,则
,则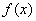 的最小值是 .
的最小值是 .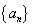 是正项等比数列,
是正项等比数列,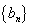 是等差数列,且
是等差数列,且 ,则有
,则有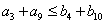 B.
B.
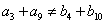 D.
D.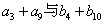 大小不确定
大小不确定 是三角形的一个内角,且
是三角形的一个内角,且 ,则这个三角形是 ( )
,则这个三角形是 ( )