题目内容
若椭圆
+y2=1（m＞1）和双曲线
-y2=1（n＞0）有共同的焦点F1、F2，且PF1⊥PF2，P是两条曲线的一个交点，则△PF1F2的面积是：（ ）
| x2 |
| m |
| x2 |
| n |
| A、2 | ||
B、
| ||
| C、2n | ||
| D、1 |
考点：椭圆的简单性质
专题：计算题,解三角形,圆锥曲线的定义、性质与方程
分析：设|PF1|=s，|PF2|=t，不妨取点P在双曲线的右支上．由双曲线和椭圆的定义可得可得s-t=2
，s+t=2
，又由于两曲线由相同的焦点，可得m-1=n+1，联立解得，再由三角形的面积公式即可得到．
| n |
| m |
解答：
解：设|PF1|=s，|PF2|=t，不妨取点P在双曲线的右支上．
由题意可得s-t=2
，①s+t=2
，②m-1=n+1，③
由②2-①2得4st=4（m-n），化为st=m-n，
把③代入可得st=2．
则△PF1F2的面积为：
st=1．
故选D．
由题意可得s-t=2
| n |
| m |
由②2-①2得4st=4（m-n），化为st=m-n，
把③代入可得st=2．
则△PF1F2的面积为：
| 1 |
| 2 |
故选D．
点评：本题考查了双曲线和椭圆的定义及其性质，考查三角形的面积公式，考查运算能力，属于中档题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知二次不等式ax2+2x+b＞0的解集为{x|x≠-
}，且a＞b，则
的最小值是（ ）
| 1 |
| a |
| a2+b2 |
| a-b |
A、2
| ||
B、2
| ||
C、3
| ||
D、3
|
已知a，b均为单位向量，其夹角为θ，有下列四个命题
p1：|a+b|＞1?θ∈[0，
）
p2：|a+b|＞1?θ∈（
，π]
p3：|a-b|＞1?θ∈[0，
）
p4：|a-b|＞1?θ∈（
，π]
其中真命题是（ ）
p1：|a+b|＞1?θ∈[0，
| 2π |
| 3 |
p2：|a+b|＞1?θ∈（
| 2π |
| 3 |
p3：|a-b|＞1?θ∈[0，
| π |
| 3 |
p4：|a-b|＞1?θ∈（
| π |
| 3 |
其中真命题是（ ）
| A、p1，p4 |
| B、p1，p3 |
| C、p2，p3 |
| D、p2，p4 |
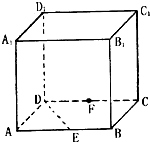正方体ABCD-A1B1C1D1的棱长为a，E是棱AB的中点，F是棱CD的中点．如果实数x，y满足条件
，那么2x-y的最大值为（ ）
|
| A、-1 | B、-2 | C、2 | D、1 |