题目内容
解下列不等式：
（1）|3x-4|＜x-1；
（2）|3x-4|＞2x-1．
（1）|3x-4|＜x-1；
（2）|3x-4|＞2x-1．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（1）去绝对值可化不等式|3x-4|＜x-1为
或
，分别解不等式组可答案；
（2）去绝对值可化不等式|3x-4|＞2x-1为
或
，分别解不等式组可得答案．
|
|
（2）去绝对值可化不等式|3x-4|＞2x-1为
|
|
解答：
解：（1）不等式|3x-4|＜x-1等价于
或
，
分别解不等式组可得
≤x＜
，或
＜x＜
，
综合可得
＜x＜
，即解集为{x|
＜x＜
}；
（2）不等式|3x-4|＞2x-1等价于
或
，
分别解不等式组可得x＞3，或x＜1，
∴不等式的解集为{x|x＜1或x＞3}
|
|
分别解不等式组可得
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 4 |
| 4 |
| 3 |
综合可得
| 5 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
（2）不等式|3x-4|＞2x-1等价于
|
|
分别解不等式组可得x＞3，或x＜1，
∴不等式的解集为{x|x＜1或x＞3}
点评：本题考查绝对值不等式，去绝对值化为不等式组是解决问题的关键，属基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知m是两个正数2，8的等比中项，则圆锥曲线x+
=1的离心率为（ ）
| y2 |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
两条直线λ1：ax-y=-2，与λ2：2x+6y+c=0相交于点（1，m），且λ1到λ2的角为
π，则a+c+m=（ ）
| 3 |
| 4 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-14 |
a，b是两条异面直线，且a⊥平面α，b⊥平面β，则α，β的关系是（ ）
| A、相交 | B、平行 |
| C、相交或平行 | D、垂直 |
若一个正三棱柱的三视图及其尺寸如图（单位：cm），则该几何体的体积（ ） cm3．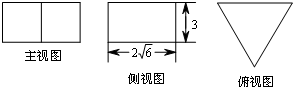
A、12
| ||
B、12
| ||
C、24
| ||
D、24
|