题目内容
6.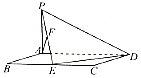 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.(1)求证:PA⊥平面ABCD;
(2)求直线BF与平面AFD所成角的正弦值.
分析 (1)利用勾股定理的逆定理得出AE⊥DE,由AF⊥平面PED得DE⊥AF,故而DE⊥平面PAE,于是DE⊥PA,结合PA⊥AD得出PA⊥平面ABCD;
(2)以E为原点建立空间坐标系,求出平面ADF的法向量$\overrightarrow{n}$,则|cos<$\overrightarrow{BF},\overrightarrow{n}$>|为直线BF与平面AFD所成角的正弦值.
解答  解:(1)连接AE,
解:(1)连接AE,
∵AF⊥平面PED,ED?平面PED,
∴AF⊥ED,
在平行四边形ABCD中,BC=2AB=4,∠ABC=60°,
∴AE=2,$ED=2\sqrt{3}$,
∴AE2+ED2=AD2,∴AE⊥ED,
又∵AF∩AE=A,AF?平面PAE,PA?平面PAE,
∴ED⊥平面PAE,∵PA?平面PAE,
∴ED⊥PA,
又PA⊥AD,AD∩ED=D,AE?平面ABCD,AD?平面ABCD,
∴PA⊥平面ABCD.
(2)以E为坐标原点,以EA,ED为x轴,y轴建立如图所示的空间直角坐标系,
则A(0,2,0),$D({2\sqrt{3},0,0})$,$B({-\sqrt{3},1,0})$,
∵AF⊥平面PED,所以AF⊥PE,
又F为PE中点,∴PA=AE=2,
∴P(0,2,2),F(0,1,1),
∴$\overrightarrow{AF}=({0,-1,1})$,$\overrightarrow{AD}=({2\sqrt{3},-2,0})$,$\overrightarrow{BF}=({\sqrt{3},0,1})$,
设平面AFD的法向量为$\overrightarrow n=({x,y,z})$,
由$\overrightarrow{AF}•\overrightarrow n=0$,$\overrightarrow{AD}•\overrightarrow n=0$得,$\left\{\begin{array}{l}-y+z=0\\ 2\sqrt{3}x-2y=0\end{array}\right.$,
令x=1,得$\overrightarrow n=({1,\sqrt{3},\sqrt{3}})$.
设直线BF与平面AFD所成的角为θ,则:$sinθ=|{cos<\overrightarrow{BF},\overrightarrow n>}|=\frac{{|{\overrightarrow{BF}•\overrightarrow n}|}}{{|{\overrightarrow{BF}}||{\overrightarrow n}|}}=\frac{{2\sqrt{3}}}{{2×\sqrt{7}}}=\frac{{\sqrt{21}}}{7}$,
即直线BF与平面AFD所成角的正弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查了线面垂直的判定,空间向量与线面角的计算,属于中档题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
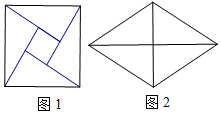 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
| A. | (0,+∞) | B. | (1,2) | C. | (2,+∞) | D. | (-∞,0) |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (2,+∞) |
| A. | 3 | B. | -3 | C. | -$\frac{3}{4}$ | D. | -$\frac{11}{4}$ |