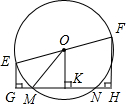
 如图,EF是圆O的直径,OE=5cm,弦MN=8cm,则E,F两点到直线MN距离的和等于( )
如图,EF是圆O的直径,OE=5cm,弦MN=8cm,则E,F两点到直线MN距离的和等于( )| A、12cm | B、6cm | C、8cm | D、3cm |
下列各函数中,y随x增大而增大的是( )
①y=-x+1;②y=-
(x<0);③y=x2+1;④y=2x-3.
①y=-x+1;②y=-
| 3 |
| x |
| A、①② | B、②③ | C、②④ | D、①③ |
 如图,EF是圆O的直径,OE=5cm,弦MN=8cm,则E,F两点到直线MN距离的和等于( )
如图,EF是圆O的直径,OE=5cm,弦MN=8cm,则E,F两点到直线MN距离的和等于( )| A、12cm | B、6cm | C、8cm | D、3cm |
| 3 |
| x |
| A、①② | B、②③ | C、②④ | D、①③ |