题目内容
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.
(1)发现:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:
(2)引申:当正方形AEFG旋转任意一个角度时(如图2),△ABE与△ADG的面积关系是:
分析:(1)根据面积公式可直接看出△ABE与△ADG是等底等高的关系,所以面积相等;
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q.利用正方形和直角三角形的性质可证明△AEP≌△AGQ,即EP=QG,AB=AD,所以△ABE与△ADG也是等底等高,它们的面积关系是相等.
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,过点G作△ADG中AD边上的高,交AD延长线于点Q.利用正方形和直角三角形的性质可证明△AEP≌△AGQ,即EP=QG,AB=AD,所以△ABE与△ADG也是等底等高,它们的面积关系是相等.
解答: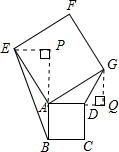 解:(1)相等,
解:(1)相等,
(2)过点E作△ABE中AB边上的高,交BA延长线于点P,
过点G作△ADG中AD边上的高,交AD延长线于点Q,
∵正方形ABCD和正方形AEFG中,内角都是直角,
∴∠EAP+∠GAP=90°,
∠QAG+∠GAP=90°,
∴∠EAP=∠DAG,
∵在正方形AEFG中,AE=AG,
在Rt△AEP和Rt△AGQ中,
∵
,
∴Rt△AEP≌Rt△AGQ(AAS),
∴EP=QG,
∵正方形ABCD中,AB=AD,
∴S△ABE=
AB×EP=S△ADG=
AD×QD.
 解:(1)相等,
解:(1)相等,(2)过点E作△ABE中AB边上的高,交BA延长线于点P,
过点G作△ADG中AD边上的高,交AD延长线于点Q,
∵正方形ABCD和正方形AEFG中,内角都是直角,
∴∠EAP+∠GAP=90°,
∠QAG+∠GAP=90°,
∴∠EAP=∠DAG,
∵在正方形AEFG中,AE=AG,
在Rt△AEP和Rt△AGQ中,
∵
|
∴Rt△AEP≌Rt△AGQ(AAS),
∴EP=QG,
∵正方形ABCD中,AB=AD,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查旋转,全等三角形的判定,正方形的性质等知识在几何综合题中运用.旋转前后许多线段相等,要掌握全等的判定方法,并会根据全等的性质和正方形的性质求得相等的线段或角.

练习册系列答案
相关题目
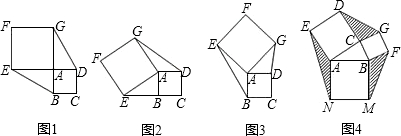
 24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.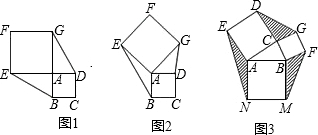
 如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.
如图,已知正方形ABCD和EFCG,点E、F、G分别在线段AC、BC、CD上,正方形ABCD的边长为6.