0 324415 324423 324429 324433 324439 324441 324445 324451 324453 324459 324465 324469 324471 324475 324481 324483 324489 324493 324495 324499 324501 324505 324507 324509 324510 324511 324513 324514 324515 324517 324519 324523 324525 324529 324531 324535 324541 324543 324549 324553 324555 324559 324565 324571 324573 324579 324583 324585 324591 324595 324601 324609 366461
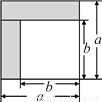

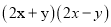 =________;
=________; 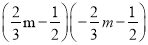 =________.
=________.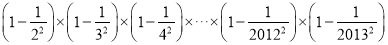
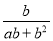 的结果为( )
的结果为( )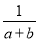 B.
B. 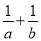 C.
C. 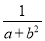 D.
D. 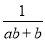
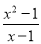 的值为零,则x的值为( )
的值为零,则x的值为( )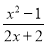 的值为0,则x的值是( )
的值为0,则x的值是( )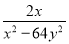 -
-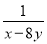 的值为( )
的值为( )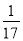 B.
B. 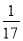 C.
C. 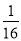 D.
D. 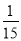
 B.
B. 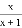 C.
C. 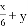 D.
D. 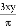
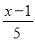 =10;②x-
=10;②x-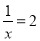 ;③
;③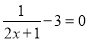 ;④
;④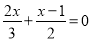 .属于分式方程的有( )
.属于分式方程的有( )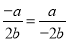 B.
B. 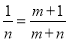 C.
C. 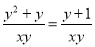 D.
D. 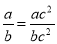
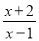 有意义,则x应满足条件( )
有意义,则x应满足条件( )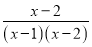 有意义,x应满足的条件是( )
有意义,x应满足的条件是( )