如果函数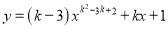 是二次函数,那么
是二次函数,那么 的值一定是( )
的值一定是( )
A. 0 B. 3 C. 0或3 D. 1或2
 A
【解析】试题分析:根据二次函数的定义,得:
k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
故选A.
A
【解析】试题分析:根据二次函数的定义,得:
k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
故选A. 在半径为4cm 的圆中,挖去一个半径为xcm 的圆面,剩下一个圆环的面积为ycm2,则y与x的函数关系式为( )
A.y=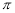 x2-4 B.y=
x2-4 B.y=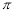 (2-x)2 C.y=-(x2+4) D.y=-
(2-x)2 C.y=-(x2+4) D.y=-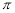 x2+16
x2+16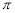
 D
【解析】
试题分析:由题意用大圆的面积减去小圆的面积即可得到结果.
由题意得y与x的函数关系式为y=-x2+16,故选D.
D
【解析】
试题分析:由题意用大圆的面积减去小圆的面积即可得到结果.
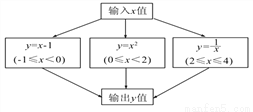
由题意得y与x的函数关系式为y=-x2+16,故选D. 根据下图所示程序计算函数值,若输入的x的值为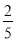 ,则输出的函数值为( )
,则输出的函数值为( )
A. 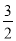 B.
B. 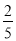 C.
C.  D.
D. 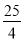
 C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C.
C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C. 某校九(1)班共有x名学生,在毕业典礼上每两名同学都握一次手,共握手y次,试写出y与x之间的函数关系式_____________,它______(填“是”或“不是”)二次函数.
 y=x2- 是
【解析】试题分析:设有x人参加聚会,每个人需要和另外的(x-1)个人握手,所以共握手x(x?1) 次,所以y=x(x?1)=x2-,是二次函数.
故答案为:y=x2-,是.
y=x2- 是
【解析】试题分析:设有x人参加聚会,每个人需要和另外的(x-1)个人握手,所以共握手x(x?1) 次,所以y=x(x?1)=x2-,是二次函数.
故答案为:y=x2-,是. 某人乘雪橇沿如图所示的斜坡笔直下滑,滑下的距离s(m)与时间t(s)之间的关系式是s=t2+10t.若下滑的时间为2s,则此人下滑的高度是_______m.
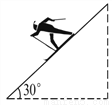
 12
【解析】试题分析:把t=2代入s= t2+10t中得:
s=24,
∵三角形是含30°角的直角三角形,
∴此人下滑的高度为:24×=12米.
故答案为12.
12
【解析】试题分析:把t=2代入s= t2+10t中得:
s=24,
∵三角形是含30°角的直角三角形,
∴此人下滑的高度为:24×=12米.
故答案为12. 函数y=(m+2) 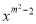 +2x-1(x≠0),当m=___时,它是二次函数,当m=_________时,它为一次函数.
+2x-1(x≠0),当m=___时,它是二次函数,当m=_________时,它为一次函数.
 2, ±或-2
【解析】试题分析:令m2-2=2,得m=2或-2,
∵m+2≠0,m≠-2,
∴m=2,
即m=2时是二次函数;
当m=-2时,y=2x-1,是一次函数,
当m2-2=1,即m=时, 是一次函数,
即m=或-2时, 是一次函数.
故答案为2; 或-2.
2, ±或-2
【解析】试题分析:令m2-2=2,得m=2或-2,
∵m+2≠0,m≠-2,
∴m=2,
即m=2时是二次函数;
当m=-2时,y=2x-1,是一次函数,
当m2-2=1,即m=时, 是一次函数,
即m=或-2时, 是一次函数.
故答案为2; 或-2. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用为1000元/m2.设矩形的一边长为xm,面积为ym2.
(1)求出y与x之间的函数关系式,说明y是不是x的二次函数,并确定x的取值范围;
(2)若x=3时,广告牌的面积最大,求此时的广告费应为多少?
 (1)y=-x2+6x,是,0<x<6 ;(2)9000元
【解析】试题分析:
(1)矩形的一边长为xm,根据矩形的周长是12m,可得矩形的另一边长为(6-x)m,根据矩形的面积公式即可得出y与x之间的函数表达式;
(2)把x=3代入函数的解析式得出y的值即为广告牌的最大面积,再乘以1000即为此时的广告费.
试题解析:
【解析】
(1)由题意得出:y =x(6-x...
(1)y=-x2+6x,是,0<x<6 ;(2)9000元
【解析】试题分析:
(1)矩形的一边长为xm,根据矩形的周长是12m,可得矩形的另一边长为(6-x)m,根据矩形的面积公式即可得出y与x之间的函数表达式;
(2)把x=3代入函数的解析式得出y的值即为广告牌的最大面积,再乘以1000即为此时的广告费.
试题解析:
【解析】
(1)由题意得出:y =x(6-x... 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h=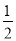 gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?
gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?
 无危险
【解析】试题分析:求出炸弹下落的时间,再算出人在此时间跑出的路程,和50米比较大小即可.
试题解析:
【解析】
无危险,
当h=490时,490=×9.8×t2,解得:t=10秒,
此时人跑的路程为:6×10=60米>50米,
所以此人无危险.
无危险
【解析】试题分析:求出炸弹下落的时间,再算出人在此时间跑出的路程,和50米比较大小即可.
试题解析:
【解析】
无危险,
当h=490时,490=×9.8×t2,解得:t=10秒,
此时人跑的路程为:6×10=60米>50米,
所以此人无危险. 某超市购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个.如果超市将篮球售价定为x元(x>50),每月销售这种篮球获利y元.
(1)求y与x之间的函数关系式;
(2)超市计划下月销售这种篮球获利8000元,又要吸引更多的顾客,那么这种篮球的售价应定为多少元?
 (1) y=-10x2+1400x-40000,50<x<100;(2)60元.
【解析】试题分析:(1)根据利润问题的数量关系,利润=售价-进价就可以得出每个篮球的利润,设销售这批篮球的利润为y元,根据销售问题的数量关系表示出y与x之间的函数关系式;
(2)令函数值y=8000,求得合适的x的值即可.
试题解析:
【解析】
(1)由题意,篮球售价定为x元,得每个篮球所获...
(1) y=-10x2+1400x-40000,50<x<100;(2)60元.
【解析】试题分析:(1)根据利润问题的数量关系,利润=售价-进价就可以得出每个篮球的利润,设销售这批篮球的利润为y元,根据销售问题的数量关系表示出y与x之间的函数关系式;
(2)令函数值y=8000,求得合适的x的值即可.
试题解析:
【解析】
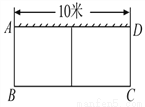
(1)由题意,篮球售价定为x元,得每个篮球所获... 如图,有一个长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为45平方米的花圃,那么AB的长为多少米?
 (1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这...
(1)S=-3x2+24x(≤x<8);(2)5米
【解析】试题分析:
(1)可先用x表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
试题解析:
【解析】
(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这...