��Ŀ����
����y��(m��2) 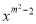 ��2x��1(x��0)����m��___ʱ�����Ƕ��κ�������m��_________ʱ����Ϊһ�κ�����
��2x��1(x��0)����m��___ʱ�����Ƕ��κ�������m��_________ʱ����Ϊһ�κ�����
 2�� ����2
�������������������m2��2��2����m��2��2��
��m��2��0��m�٣�2��
��m��2��
��m��2ʱ�Ƕ��κ�����
��m����2ʱ��y��2x��1����һ�κ�����
��m2��2��1����m��ʱ�� ��һ�κ�����
��m����2ʱ�� ��һ�κ�����
�ʴ�Ϊ2�� ��2��
2�� ����2
�������������������m2��2��2����m��2��2��
��m��2��0��m�٣�2��
��m��2��
��m��2ʱ�Ƕ��κ�����
��m����2ʱ��y��2x��1����һ�κ�����
��m2��2��1����m��ʱ�� ��һ�κ�����
��m����2ʱ�� ��һ�κ�����
�ʴ�Ϊ2�� ��2��
 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д���֪M= ��N=
��N= ����a��1����M��N�Ĵ�С��ϵΪ( )
����a��1����M��N�Ĵ�С��ϵΪ( )
A. M��N B. M��N C. M��N D. M��N
 C
����������M����N����
��M-N��-
��
��
��-��0,
��M��N.
��ѡC.
C
����������M����N����
��M-N��-
��
��
��-��0,
��M��N.
��ѡC. ���������ε�һ������80�㣬�����Ķ��ǵĶ����ǣ����� ��
A. 80�� B. 80���20�� C. 80���50�� D. 20��
 B
�������������������80����Ƕ�������������������⣮ ��80����Ƕ���ʱ�������εĶ���Ϊ80�㣬
��80����ǵ�ʱ������Ϊ180�㩁80���2=20�㣬 �����������õ��������ζ��ǵĶ���Ϊ80���20�㣮
B
�������������������80����Ƕ�������������������⣮ ��80����Ƕ���ʱ�������εĶ���Ϊ80�㣬
��80����ǵ�ʱ������Ϊ180�㩁80���2=20�㣬 �����������õ��������ζ��ǵĶ���Ϊ80���20�㣮 ��ͼ��AB=AD��CB=CD��AC��BD�ཻ�ڵ�O�������н�����ȷ���ǣ� ��

A. OA=OC B. ��O��AB��CD�ľ������
C. ��BDA=��BDC D. ��O��CB��CD�ľ������
 D
�����������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��
���DCA=��BCA��
���O��CB��CD�ľ������.
��ѡD.
D
�����������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��
���DCA=��BCA��
���O��CB��CD�ľ������.
��ѡD. ��ͼ��ֱ��l1��l2��l3��ʾ���������Ĺ�·����Ҫ��һ��������תվ��Ҫ������������·�ľ�����ȣ���ɹ�ѡ��ĵ�ַ�У�������

A. 1�� B. 2�� C. 3�� D. 4��
 D
����������ͼA��B��C��DΪ����ֱ����ɵ��������ڽǺ���ǵĽ�ƽ���ߵĽ��㣬�ɽ�ƽ�����ϵĵ㵽�����߾�����ȿɵ������ĵ㴦��������תվ��������·�������.
��ѡD.
D
����������ͼA��B��C��DΪ����ֱ����ɵ��������ڽǺ���ǵĽ�ƽ���ߵĽ��㣬�ɽ�ƽ�����ϵĵ㵽�����߾�����ȿɵ������ĵ㴦��������תվ��������·�������.
��ѡD. �������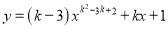 �Ƕ��κ�������ô
�Ƕ��κ�������ô ��ֵһ����( )
��ֵһ����( )
A. 0 B. 3 C. 0��3 D. 1��2
 A
��������������������ݶ��κ����Ķ��壬�ã�
k2��3k��2��2��
���k��0��k��3��
�֡�k��3��0��
��k��3��
�൱k��0ʱ����������Ƕ��κ�����
��ѡA��
A
��������������������ݶ��κ����Ķ��壬�ã�
k2��3k��2��2��
���k��0��k��3��
�֡�k��3��0��
��k��3��
�൱k��0ʱ����������Ƕ��κ�����
��ѡA�� 1022����_______��
 10404
��������1022=��100+2��2=10000+400+4=10404.
10404
��������1022=��100+2��2=10000+400+4=10404. ��x+5y��2 ���ڣ� ��
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
��������������ȫƽ����ʽ�ɵã���x+5y��2=x2+10xy+25y 2 ����ѡC.
C
��������������ȫƽ����ʽ�ɵã���x+5y��2=x2+10xy+25y 2 ����ѡC. ����ƽ��ֱ������ϵ����������M��x1�� y1����N��x2��y2������|x1��x2|+|y1��y2|ΪM��N����Ĺ��ɾ��룬������d��M��N�����磺M��2����3����N��1��4������d��M��N��=|2��1|+|��3��4|=8. ��P��x0��y0����һ���㣬Q��x��y����ֱ��y=kx+b�ϵ�һ���㣬��d��P��Q������СֵΪP��ֱ��y=kx+b�Ĺ��ɾ��룮��P��-3,2����ֱ��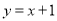 �Ĺ��ɾ���Ϊ�� ��
�Ĺ��ɾ���Ϊ�� ��
A. 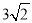 B.
B. 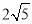 C. 3 D. 4
C. 3 D. 4
 D
�����������ݴ��߶���̣��ɵõ�PQֱ��ʱ��PQ��̣���PQ �Ľ���ʽΪy=-x+b����P��-3,2���������b=-1������PQ �Ľ���ʽΪy=-x-1����-x-1=x+1�����x=-1.��x=-1����y=x+1��y=0�����ɵõ�Q������Ϊ��-1,0��������P��-3,2����ֱ�ߵĹ��ɾ���Ϊ|-3����-1����|+|2��0|=2+2=4����ѡD.
D
�����������ݴ��߶���̣��ɵõ�PQֱ��ʱ��PQ��̣���PQ �Ľ���ʽΪy=-x+b����P��-3,2���������b=-1������PQ �Ľ���ʽΪy=-x-1����-x-1=x+1�����x=-1.��x=-1����y=x+1��y=0�����ɵõ�Q������Ϊ��-1,0��������P��-3,2����ֱ�ߵĹ��ɾ���Ϊ|-3����-1����|+|2��0|=2+2=4����ѡD. 
