题目内容
物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h=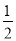 gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?
gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?
 无危险
【解析】试题分析:求出炸弹下落的时间,再算出人在此时间跑出的路程,和50米比较大小即可.
试题解析:
【解析】
无危险,
当h=490时,490=×9.8×t2,解得:t=10秒,
此时人跑的路程为:6×10=60米>50米,
所以此人无危险.
无危险
【解析】试题分析:求出炸弹下落的时间,再算出人在此时间跑出的路程,和50米比较大小即可.
试题解析:
【解析】
无危险,
当h=490时,490=×9.8×t2,解得:t=10秒,
此时人跑的路程为:6×10=60米>50米,
所以此人无危险.
练习册系列答案
相关题目
(2016内蒙古包头市)化简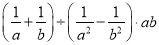 ,其结果是( )
,其结果是( )
A. 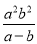 B.
B. 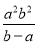 C.
C. 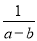 D.
D. 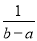
 B
【解析】= .
所以选B.
B
【解析】= .
所以选B. 等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A. 7 B. 11 C. 7或11 D. 7或10
 C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
...
C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
... 三角形中∠B的平分线和外角的平分线的夹角是( ).
A. 60° B. 90° C. 45° D. 135°
 B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B.
B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
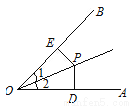
A. PD=PE B. OD=OE C. ∠DPO=∠EPO D. PD=OP
 D
【解析】试题分析:根据角平分线的性质可得:PD=PE,根据题意HL判定定理可得:Rt△POE≌Rt△POD,则OD=OE,∠DPO=∠EPO.
D
【解析】试题分析:根据角平分线的性质可得:PD=PE,根据题意HL判定定理可得:Rt△POE≌Rt△POD,则OD=OE,∠DPO=∠EPO. 根据下图所示程序计算函数值,若输入的x的值为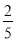 ,则输出的函数值为( )
,则输出的函数值为( )
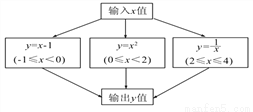
A. 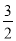 B.
B. 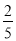 C.
C.  D.
D. 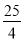
 C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C.
C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C. 982+(a-b)2
 9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2.
9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2. (x+5y)2 等于( )
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C.
C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C. 已知点M(2m -3,8),N(m -1,-3),且MN//y轴,则m=________.
 2
【解析】由MN//y轴,可得点M、N的横坐标相同,即2m-3=m-1,解得m=2.
2
【解析】由MN//y轴,可得点M、N的横坐标相同,即2m-3=m-1,解得m=2. 
