甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.
（1）甲、乙所购饲料的平均单价各是多少？
（2）谁的购货方式更合算？
（1）甲的平均单价为元/千克，乙平均单价为元/千克；（2）乙的购货方式更合算.
【解析】【试题分析】（1）设第一次饲料的价格为x元/千克，第二次饲料的价格为y元/千克，根据平均价格= ，代入即可.则这两次所购饲料的平均单价元/千克.则甲的平均单价为 元/千克；乙所购的饲料的平均单价为 元/千克.
(2)利用作差法比较大小即可.得： ，由于 ，得乙的购货方式更合算.
【试题解析... 为进一步落实《中华人民共和国民办教育促进法》，某市教育局拿出了b元资金建立民办教育发展基金会，其中一部分作为奖金发给了n所民办学校．奖金分配方案如下：首先将n所民办学校按去年完成教育、教学工作业绩（假设工作业绩均不相同）从高到低，由1到n排序，第1所民办学校得奖金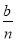
元，然后再将余额除以n发给第2所民办学校，按此方法将奖金逐一发给了n所民办学校．
（1）请用n、b分别表示第2所、第3所民办学校得到的奖金；
（2）设第k所民办学校所得到的奖金为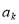
元（1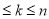 
），试用k、n和b表示
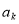（不必证明）；
（3）比较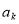
和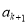
的大小（k=1，2 ，……， 
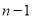），并解释此结果关于奖金分配原则的实际意义．
（1） , ；
（2） ；
（3） ．奖金分配的实际意义：名次越靠后，奖金越少．
【解析】【试题分析】
（1）根据第1所民办学校得奖金元，然后再将余额除以n发给第2所民办学校，得：
（2）根据（1）中的两个式子， ；
（3）， ，则，则.奖金分配的实际意义：名次越靠后，奖金越少.
【试题解析】
（1）根据题意得：
（2）根据（1）中的两个式子，... 某学生在计算四个多边形的内角和时，得到下列四个答案，其中错误的是（ ）
A. 180° B. 540° C. 1900° D. 1080°
C
【解析】多边形的内角和公式是(n-2)•180°，内角和是180°时候是三角形；内角和是540°时候是五边形；内角和是1080°的时候是十边形，内角和是1900°时候算出来的边数不是整数，所以错误的是C，
故选C. 如果一个多边形的内角和是720°，那么这个多边形的对角线的条数是（ ）
A. 6 B. 9 C. 14 D. 20
B
【解析】设多边形的边数为n，则有：(n-2)•180°=720°，解得：n=6，
所以这个多边形的对角线的条数是==9，
故选B. 一个多边形中，除一个内角外，其余各内角和是120°，则这个角的度数是（ ）
A. 60° B. 80° C. 100° D. 120°
A
【解析】根据多边形的内角和公式可以知道，多边形的内角和是180°的正整数倍，所以只有A选项和120°相加是180°的正整数倍，
故选A. 一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A. 10 B. 12 C. 6 D. 7
B
【解析】设这个多边形的边数为n，由题意则有
(n-2)•180°=360°×5，
解得n=12，
故选B. 若一个多边形除了一个内角外,其余各内角之和是2570°,则这个角是( )
A. 90° B. 15° C. 120° D. 130°
D
【解析】设这个内角度数为x°，边数为n，
则（n-2）×180-x=2570，
180•n=2930+x，
∵n为正整数，
∴n=17，
∴去掉角度数为180°×（17-2）-2570°=130°，
故选D. 在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
B
【解析】多边形的外角和是360°，因此外角中最多有三个钝角，外角与相邻的内角互为邻补角，
所以在多边形的内角中，锐角的个数不能多于3个，
故选B. n边形的边数增加一倍,它的内角和增加( )
A. 180° B. 360° C. (n-2)·180° D. n180°
D
【解析】∵n边形的内角和是（n-2）•180°，
∴2n边形的内角和是（2n-2）•180°，
∴将n边形的边数增加一倍，则它的内角和增加：（2n-2）•180°-（n-2）•180°=n180°，
故选D. 用下列一种正多边形可以拼地板的是（ ）
A． 正五边形 B． 正六边形 C． 正八边形 D． 正十二边形
B
【解析】
试题分析：先计算各正多边形每一个内角的度数，判断是否为360°的约数．
【解析】
A、正五边形的每一个内角度数为180°﹣360°÷5=108°，108°不是360°的约数，故一种正五边形不能拼地板；
B、正六边形的每一个内角度数为180°﹣360°÷6=120°，120°是360°的约数，故一种六边形能拼地板；
C、正八边形的每一个内角度数为180°...