题目内容
用下列一种正多边形可以拼地板的是（ ）
A． 正五边形 B． 正六边形 C． 正八边形 D． 正十二边形
B
【解析】
试题分析：先计算各正多边形每一个内角的度数，判断是否为360°的约数．
【解析】
A、正五边形的每一个内角度数为180°﹣360°÷5=108°，108°不是360°的约数，故一种正五边形不能拼地板；
B、正六边形的每一个内角度数为180°﹣360°÷6=120°，120°是360°的约数，故一种六边形能拼地板；
C、正八边形的每一个内角度数为180°...
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图所示，已知二次函数y＝ax2+bx+c(a≠0)的图象的顶点p的横坐标是4，图象与x轴交于点A(m，0)和点B，且点A在点B的左侧，那么线段AB的长是____．(用含字母m的代数式表示)
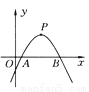
8－2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4，
所以抛物线对称轴所在直线为x=4，交x轴于点D，
所以A.B两点关于对称轴对称，
因为点A(m,0)，且m<4，即AD=4-m，
所以AB=2AD=2(4-m)=8-2m，
故答案为：8-2m. 在□ABCD中，对角线AC，BD相交于点O，AB=8cm，BC=6cm．△AOB的周长是18cm，则△AOD的周长是__________．
16cm
【解析】试题解析：
如图所示：
∵四边形ABCD是平行四边形，
的周长是18cm，AB=8cm，
的周长
故答案为：16cm． 如图，在?ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（ ）
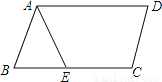
A．8cm B．6cm C．4cm D．2cm
C
【解析】
试题分析：【解析】
∵四边形ABCD是平行四边形，
∴BC=AD=12cm，AD∥BC，
∴∠DAE=∠BEA，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BEA=∠BAE，
∴BE=AB=8cm，
∴CE=BC﹣BE=4cm；
故答案为：C． 一个多边形的每个外角都是36°，这个多边形是______边形
十
【解析】∵任何多边形的外角和等于360°，
∴多边形的边数为360°÷36°=10，
故答案为：十. 一个多边形中，除一个内角外，其余各内角和是120°，则这个角的度数是（ ）
A. 60° B. 80° C. 100° D. 120°
A
【解析】根据多边形的内角和公式可以知道，多边形的内角和是180°的正整数倍，所以只有A选项和120°相加是180°的正整数倍，
故选A. 解方程:
.
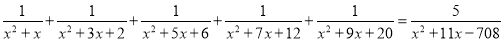x=118
【解析】【试题分析】用拆项法解方程， = 将方程左边化简为= ，再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根. 如果方程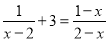
有增根， 那么增根是_______．
x=2
【解析】∵原方程有增根，
∴最简公分母x-2=0，
解得x=2，
故答案为：x=2. 解下列方程：
（1）1﹣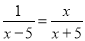
（2）
．
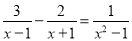(1) ;(2)x=-5
【解析】试题分析：先去分母，把分式方程转化为整式方程，然后按照整式方程的解法求解，求出未知数的值后要验根.
【解析】
（1）去分母得：x2﹣25﹣x﹣5=x2﹣5x，
解得：x=，
经检验x=是分式方程的解；
（2）去分母得：3x+3﹣2x+3=1，
解得：x=﹣5，
经检验x=﹣5是分式方程的解．