题目内容
一个多边形中,除一个内角外,其余各内角和是120°,则这个角的度数是( )
A. 60° B. 80° C. 100° D. 120°
 A
【解析】根据多边形的内角和公式可以知道,多边形的内角和是180°的正整数倍,所以只有A选项和120°相加是180°的正整数倍,
故选A.
A
【解析】根据多边形的内角和公式可以知道,多边形的内角和是180°的正整数倍,所以只有A选项和120°相加是180°的正整数倍,
故选A.
练习册系列答案
相关题目
当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A. ﹣2 B. 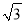 或-
或-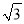 C. 2或-
C. 2或-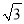 D. 2或﹣
D. 2或﹣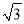 或-
或-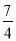
 C
【解析】由题意得该抛物线的对称轴为x=m.
①当-2≤m≤1时,此时最大值为,即=4,
解得m= (舍去)或m=-;
②当m>1时,此时当x=1时,函数有最大值,所以,
解得m=2;
③当m<-2时,此时x=-2函数有最大值,所以,
解得m= (不合题意,舍去).
综上所述,m= -或m=2.
所以C选项是正确的.
C
【解析】由题意得该抛物线的对称轴为x=m.
①当-2≤m≤1时,此时最大值为,即=4,
解得m= (舍去)或m=-;
②当m>1时,此时当x=1时,函数有最大值,所以,
解得m=2;
③当m<-2时,此时x=-2函数有最大值,所以,
解得m= (不合题意,舍去).
综上所述,m= -或m=2.
所以C选项是正确的. 如图等腰梯形ABCD,AE是BC边上的高.已知AE=4,CE=8,则梯形ABCD的面积是( )
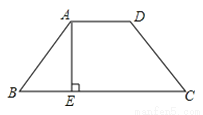
A. 16 B. 32 C. 24 D. 48
 B
【解析】试题解析:过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°.
∵四边形ABCD是等腰梯形
∴AD∥BC,AB=CD,
又∵AE是BC边上的高,
∴四边形AECF是矩形.
在和中
≌(HL).
∴梯形ABCD的面积=矩形AECF的面积=4×8=32.
故选B.
B
【解析】试题解析:过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°.
∵四边形ABCD是等腰梯形
∴AD∥BC,AB=CD,
又∵AE是BC边上的高,
∴四边形AECF是矩形.
在和中
≌(HL).
∴梯形ABCD的面积=矩形AECF的面积=4×8=32.
故选B. 如果一个多边形的内角和与它的外角和相等,那么这个多边形是____边形
 四
【解析】∵多边形的外角和为360°,
而一个多边形的内角和与它的外角和正好相等,设这个多边形为n边形,
∴(n-2)•180°=360°,
∴n=4,
故答案为:四.
四
【解析】∵多边形的外角和为360°,
而一个多边形的内角和与它的外角和正好相等,设这个多边形为n边形,
∴(n-2)•180°=360°,
∴n=4,
故答案为:四. 用下列一种正多边形可以拼地板的是( )
A. 正五边形 B. 正六边形 C. 正八边形 D. 正十二边形
 B
【解析】
试题分析:先计算各正多边形每一个内角的度数,判断是否为360°的约数.
【解析】
A、正五边形的每一个内角度数为180°﹣360°÷5=108°,108°不是360°的约数,故一种正五边形不能拼地板;
B、正六边形的每一个内角度数为180°﹣360°÷6=120°,120°是360°的约数,故一种六边形能拼地板;
C、正八边形的每一个内角度数为180°...
B
【解析】
试题分析:先计算各正多边形每一个内角的度数,判断是否为360°的约数.
【解析】
A、正五边形的每一个内角度数为180°﹣360°÷5=108°,108°不是360°的约数,故一种正五边形不能拼地板;
B、正六边形的每一个内角度数为180°﹣360°÷6=120°,120°是360°的约数,故一种六边形能拼地板;
C、正八边形的每一个内角度数为180°... 某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
 (1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,...
(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程,有:
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,... 设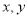 是两个不同的正整数,且
是两个不同的正整数,且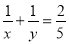 ,则
,则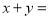 _____.
_____.
 18
【解析】根据,得:5(x+y)=2xy,
因为x、y都是整数,则 ,则
18
【解析】根据,得:5(x+y)=2xy,
因为x、y都是整数,则 ,则 当x=( )时, 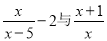 互为相反数.
互为相反数.
A. 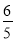 B.
B. 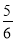 C.
C. 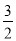 D.
D. 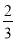
 B
【解析】由题意得: .故选B.
B
【解析】由题意得: .故选B. 若关于x的方程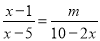 无解,则m=___________.
无解,则m=___________.
 -8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8.
-8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8. 
