题目内容
如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A. 6 B. 9 C. 14 D. 20
 B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B.
B
【解析】设多边形的边数为n,则有:(n-2)•180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
故选B.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二次函数y=ax2+bx+c满足b2=ac,且x=0时,y=﹣4,则( )
A. y最大=﹣4 B. y最小=﹣4 C. y最大=﹣3 D. y最小=﹣3
 C
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C.
C
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C. 如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
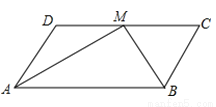
A. 100° B. 95° C. 90° D. 85°
 C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C. 若n边形的每个内角都等于150°,则n=_____.
 12
【解析】试题解析:由题意可得:
解得
故多边形是12边形.
故答案为:12.
12
【解析】试题解析:由题意可得:
解得
故多边形是12边形.
故答案为:12. n边形的边数增加一倍,它的内角和增加( )
A. 180° B. 360° C. (n-2)·180° D. n180°
 D
【解析】∵n边形的内角和是(n-2)•180°,
∴2n边形的内角和是(2n-2)•180°,
∴将n边形的边数增加一倍,则它的内角和增加:(2n-2)•180°-(n-2)•180°=n180°,
故选D.
D
【解析】∵n边形的内角和是(n-2)•180°,
∴2n边形的内角和是(2n-2)•180°,
∴将n边形的边数增加一倍,则它的内角和增加:(2n-2)•180°-(n-2)•180°=n180°,
故选D. 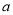 为何值时,分式方程
为何值时,分式方程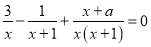 无解?
无解?
 当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
...
当或时原分式方程无解
【解析】【试题分析】方程的两边同乘以,去分母,得:
整理,得.
即,把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;当 时, ,
于是当或时原分式方程无解.
【试题解析】
方程的两边同乘以,去分母,得
整理,得。
即.
把代入最简公分母,使其值为零,说明整式方程的根是增根.
当 时, ;
... 若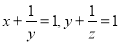 ,则
,则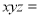 _____.
_____.
 -1
【解析】根据得: .
故答案:-1.
-1
【解析】根据得: .
故答案:-1. 下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根
D.使最简公分母的值为零的解是增根
 D
【解析】
试题分析:分式方程的增根是最简公分母为零时,未知数的值.
【解析】
分式方程的增根是使最简公分母的值为零的解.
故选D.
D
【解析】
试题分析:分式方程的增根是最简公分母为零时,未知数的值.
【解析】
分式方程的增根是使最简公分母的值为零的解.
故选D. 下列各式① ;②
;②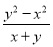 ;③
;③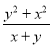 ;④
;④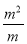 ;⑤
;⑤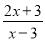 中分子与分母没有公因式的分式是__.(填序号)
中分子与分母没有公因式的分式是__.(填序号)
 ③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式.
③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式. 
