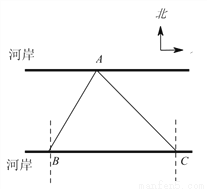
如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：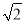 
≈1.41， 
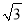≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
答：A点到BC的距离是95 m. 已知抛物线过A(－1，0)，B(3，0)两点，与y轴交于C点，且BC=3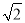
，则这条抛物线的解析式为 ( )
A. y=－x2+2x+3 B. y＝x2－2x－3
C. y=x2+2x―3或y＝－x2+2x+3 D. y=－x2+2x+3或y＝x2－2x－3
D
【解析】∵A、B两点的纵坐标为0.
∴A、B为抛物线与x轴的交点，
∴△OBC为直角三角形。
又∵C点有可能在y轴的负半轴，也可能在y轴的正半轴。
∴C点的纵坐标为3或?3(根据勾股定理求得).
∴C点的纵坐标为(0,3)或(0,?3).
设函数的解析式为y=ax²+bx+c，
(1)则当抛物线经过(?1,0)、(3,0)、(0,?3)三点时，
... 如果点(－2，－3)和(5，－3)都是抛物线y=ax2+bx+c上的点，那么抛物线的对称轴是 ( )
A. x=3 B. x=－3 C. x=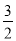
D. x=－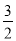
C
【解析】点(?2,?3)和(5,?3)都是抛物线y=ax²+bx+c上的点，得
(?2,?3)、(5,?3)关于对称轴对称，
即对称轴过(?2,?3)、(5,?3)的中点，
x=，
故选C. 二次函数y=ax2+bx+c满足b2=ac，且x=0时，y=﹣4，则（ ）
A. y最大=﹣4 B. y最小=﹣4 C. y最大=﹣3 D. y最小=﹣3
C
【解析】试题分析：将x=0，y=-4代入可得：c=-4，根据可得： ，故函数有最大值，则最大值为： ，故选C． 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（ ）
A. ﹣2 B.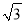 
或-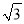
C. 2或-
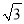D. 2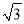或﹣
或-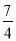
C
【解析】由题意得该抛物线的对称轴为x=m.
①当-2≤m≤1时,此时最大值为,即=4,
解得m= (舍去)或m=-;
②当m>1时,此时当x=1时,函数有最大值,所以,
解得m=2;
③当m<-2时,此时x=-2函数有最大值,所以,
解得m= (不合题意,舍去).
综上所述,m= -或m=2.
所以C选项是正确的. 平时我们在跳绳时，绳摇到最高点处的形状可近似地看做抛物线，如图所示．正在摇绳的甲、乙两名同学拿绳的手间距为4 m，距地高均为1 m，学生丙、丁分别站在距甲拿绳的手水平距离1 m，2．5 m处．绳子在摇到最高处时刚好通过他们的头顶．已知学生丙的身高是1．5 m，则学生丁的身高为 ( )
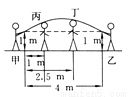
A. 1.5 m B. 1.625 m C. 1.66 m D. 1.67 m
B
【解析】设所求的函数的解析式为y=ax2+bx+c，由已知，函数的图象过（-1，1），（0，1.5），（3，1）三点，易求其解析式为y=-x2+x+,∵丁头顶的横坐标为1.5，∴代入其解析式可求得其纵坐标为1.625m.故选B. 将抛物线y=x2向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是________．
y=（x+4）2-2
【解析】∵y=x2向左平移4个单位后,再向下平移2个单位. ∴y= .故此时抛物线的解析式是y=.故答案为：y=（x+4）2-2. 已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数的表达式________．
y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为：y=x2-2. 函数y=x2+bx-c的图象经过点（1，2），则b-c的值为______．
1
【解析】∵函数y=x²+bx?c的图象经过点(1,2)，
∴把点(1,2)代入函数式，得2=1+b?c，
即b?c=1.故答案为：1. 如图所示，已知二次函数y＝ax2+bx+c(a≠0)的图象的顶点p的横坐标是4，图象与x轴交于点A(m，0)和点B，且点A在点B的左侧，那么线段AB的长是____．(用含字母m的代数式表示)
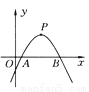
8－2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4，
所以抛物线对称轴所在直线为x=4，交x轴于点D，
所以A.B两点关于对称轴对称，
因为点A(m,0)，且m<4，即AD=4-m，
所以AB=2AD=2(4-m)=8-2m，
故答案为：8-2m.