��Ŀ����
��֪�����߹�A(��1��0)��B(3��0)���㣬��y�ύ��C�㣬��BC=3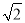 �������������ߵĽ���ʽΪ ( )
�������������ߵĽ���ʽΪ ( )
A. y=��x2+2x+3 B. y��x2��2x��3
C. y=x2+2x�D3��y����x2+2x+3 D. y=��x2+2x+3��y��x2��2x��3
 D
����������A��B�����������Ϊ0.
��A��BΪ��������x��Ľ��㣬
���OBCΪֱ�������Ρ�
�֡�C���п�����y��ĸ����ᣬҲ������y��������ᡣ
��C���������Ϊ3��?3(���ݹ��ɶ������).
��C���������Ϊ(0,3)��(0,?3).
�躯���Ľ���ʽΪy=ax²+bx+c��
(1)�������߾���(?1,0)��(3,0)��(0,?3)����ʱ��
...
D
����������A��B�����������Ϊ0.
��A��BΪ��������x��Ľ��㣬
���OBCΪֱ�������Ρ�
�֡�C���п�����y��ĸ����ᣬҲ������y��������ᡣ
��C���������Ϊ3��?3(���ݹ��ɶ������).
��C���������Ϊ(0,3)��(0,?3).
�躯���Ľ���ʽΪy=ax²+bx+c��
(1)�������߾���(?1,0)��(3,0)��(0,?3)����ʱ��
...
��������y=ax2+bx+c(a��0)����A(0��2)��B(4��3)��C���㣬���е�C��ֱ��x=2�ϣ��ҵ�C�������ߵĶԳ���ľ������1���������ߵĺ�������ʽΪ______.
 y=x2-x+2��y=-x2+x+2.
������������������������߹�A(0��2)����.
�������߹�B(4��3)����.
�������߹�C���ҵ�C��ֱ���ϣ���C�������߶Գ���ľ������1��
��.
���û�.
�������ߵĺ�������ʽΪ��.
y=x2-x+2��y=-x2+x+2.
������������������������߹�A(0��2)����.
�������߹�B(4��3)����.
�������߹�C���ҵ�C��ֱ���ϣ���C�������߶Գ���ľ������1��
��.
���û�.
�������ߵĺ�������ʽΪ��. ��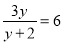 ����
����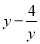 =_______.
=_______.
 -3
���������ⷽ�̣��ã�y=-4��������y=-4�Ƿ��̵Ľ⣬
����=-4+1=-3��
�ʴ�Ϊ��-3.
-3
���������ⷽ�̣��ã�y=-4��������y=-4�Ƿ��̵Ľ⣬
����=-4+1=-3��
�ʴ�Ϊ��-3. ��֪������y��ax2��b x��c����A��B��C���㣬��x��0ʱ����ͼ����ͼ��ʾ��
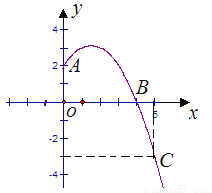
��1���������ߵĽ���ʽ��д�������ߵĶ������ꣻ
��2������������y��ax2��b x��c��x��0ʱ��ͼ��
��3������������y��ax2��b x��c��д��xΪ��ֵʱ��y��0��
 ��1��������y �����㣨������2���ԣ�3�� ����1��x��4ʱ�� y >0
���������������������Ĺؼ�����������ߵĽ���ʽ������Ŀ������ͼ���пɵó�A��B��C��������꣬���ô���ϵ����������ߵĽ���ʽ�������ɻ���x��0ʱ�����ߵ�ͼ���Լ�y��0ʱx��ȡֵ��Χ��
��������
��1����ͼ��֪A��0��2����B��4��0����C��5����3����
�÷����飮
���a=����b=��c=2��...
��1��������y �����㣨������2���ԣ�3�� ����1��x��4ʱ�� y >0
���������������������Ĺؼ�����������ߵĽ���ʽ������Ŀ������ͼ���пɵó�A��B��C��������꣬���ô���ϵ����������ߵĽ���ʽ�������ɻ���x��0ʱ�����ߵ�ͼ���Լ�y��0ʱx��ȡֵ��Χ��
��������
��1����ͼ��֪A��0��2����B��4��0����C��5����3����
�÷����飮
���a=����b=��c=2��... ��������y=x2����ƽ��4����λ��������ƽ��2����λ�����ʱ�����ߵĽ���ʽ��________��
 y=��x+4��2-2
����������y=x2����ƽ��4����λ��,������ƽ��2����λ. ��y= .�ʴ�ʱ�����ߵĽ���ʽ��y=.�ʴ�Ϊ��y=��x+4��2-2.
y=��x+4��2-2
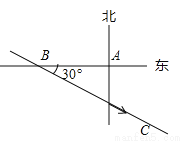
����������y=x2����ƽ��4����λ��,������ƽ��2����λ. ��y= .�ʴ�ʱ�����ߵĽ���ʽ��y=.�ʴ�Ϊ��y=��x+4��2-2. �����д��ڶ����غ����ļ���������̨��Ϯ����һ�Σ���������ֲ��̨��������������A����������300ǧ��B������ͼ������ÿСʱ10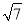 ǧ���ٶ���ƫ��30���BC�����ƶ�������̨���������ƶ������У�������A���ܵ�Ӱ�죬�Ҿ�̨������200ǧ�ķ�Χ����̨������Ӱ���������Ӱ��������A��ʱ�����������������
ǧ���ٶ���ƫ��30���BC�����ƶ�������̨���������ƶ������У�������A���ܵ�Ӱ�죬�Ҿ�̨������200ǧ�ķ�Χ����̨������Ӱ���������Ӱ��������A��ʱ�����������������
A. 5 B. 6 C. 8 D. 10
 D
���������������������A��AD��BC��D���������AB=300����ABD��30�㣬��AD =150��km����
�����е�A�ܵ�̨������Ӱ�����̨���ľ�A��200km�����պô���BC�ϵ�E��F����
����Rt��ADE��AE��200��AD��150 ��DE=50km�� ��EF=2DE=100km��
��t=100��10=10h����ѡD��
D
���������������������A��AD��BC��D���������AB=300����ABD��30�㣬��AD =150��km����
�����е�A�ܵ�̨������Ӱ�����̨���ľ�A��200km�����պô���BC�ϵ�E��F����
����Rt��ADE��AE��200��AD��150 ��DE=50km�� ��EF=2DE=100km��
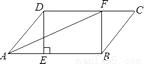
��t=100��10=10h����ѡD�� ��ƽ���ı���ABCD�У�����D��DE��AB�ڵ�E����F �ڱ�CD�ϣ�DF=BE������AF��BF��
��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF=3��BF=4��DF=5����֤��AFƽ�֡�DAB��
 ��1��֤����������2��֤��������
�������������������1������ƽ���ı��ε����ʣ��ɵ�AB��CD�Ĺ�ϵ������ƽ���ı��ε��ж����ɵ�BFDE��ƽ���ı��Σ��ٸ��ݾ��ε��ж����ɵô𰸣�
��2������ƽ���ߵ����ʣ��ɵá�DFA=��FAB�����ݵ��������ε��ж������ʣ��ɵá�DAF=��DFA�����ݽ�ƽ���ߵ��ж����ɵô𰸣�
�����������1��֤�������ı���ABCD��ƽ���ı��Σ�
��AB��C...
��1��֤����������2��֤��������
�������������������1������ƽ���ı��ε����ʣ��ɵ�AB��CD�Ĺ�ϵ������ƽ���ı��ε��ж����ɵ�BFDE��ƽ���ı��Σ��ٸ��ݾ��ε��ж����ɵô𰸣�
��2������ƽ���ߵ����ʣ��ɵá�DFA=��FAB�����ݵ��������ε��ж������ʣ��ɵá�DAF=��DFA�����ݽ�ƽ���ߵ��ж����ɵô𰸣�
�����������1��֤�������ı���ABCD��ƽ���ı��Σ�
��AB��C... Ϊ��һ����ʵ���л������������ٽ�������ij�н������ó���bԪ�ʽ�����������չ����ᣬ����һ������Ϊ������n�����ѧУ��������䷽�����£����Ƚ�n�����ѧУ��ȥ����ɽ�������ѧ����ҵ�������蹤��ҵ��������ͬ���Ӹߵ��ͣ���1��n����1�����ѧУ�ý���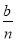 Ԫ��Ȼ���ٽ�������n������2�����ѧУ�����˷�����������һ������n�����ѧУ��
Ԫ��Ȼ���ٽ�������n������2�����ѧУ�����˷�����������һ������n�����ѧУ��
��1������n��b�ֱ��ʾ��2������3�����ѧУ�õ��Ľ���
��2�����k�����ѧУ���õ��Ľ���Ϊ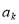 Ԫ��1
Ԫ��1 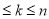 ��������k��n��b��ʾ
��������k��n��b��ʾ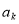 ������֤������
������֤������
��3���Ƚ�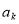 ��
��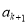 �Ĵ�С��k=1��2 ��������
�Ĵ�С��k=1��2 �������� 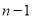 ���������ʹ˽�����ڽ������ԭ���ʵ�����壮
���������ʹ˽�����ڽ������ԭ���ʵ�����壮
 ��1�� , ��
��2�� ��
��3�� ����������ʵ�����壺����Խ������Խ�٣�
�������������������
��1�����ݵ�1�����ѧУ�ý���Ԫ��Ȼ���ٽ�������n������2�����ѧУ���ã�
��2�����ݣ�1���е�����ʽ�ӣ� ��
��3���� ������.��������ʵ�����壺����Խ������Խ��.
�����������
��1����������ã�
��2�����ݣ�1���е�����ʽ�ӣ�...
��1�� , ��
��2�� ��
��3�� ����������ʵ�����壺����Խ������Խ�٣�
�������������������
��1�����ݵ�1�����ѧУ�ý���Ԫ��Ȼ���ٽ�������n������2�����ѧУ���ã�
��2�����ݣ�1���е�����ʽ�ӣ� ��
��3���� ������.��������ʵ�����壺����Խ������Խ��.
�����������
��1����������ã�
��2�����ݣ�1���е�����ʽ�ӣ�... 
