题目内容
如图所示，已知二次函数y＝ax2+bx+c(a≠0)的图象的顶点p的横坐标是4，图象与x轴交于点A(m，0)和点B，且点A在点B的左侧，那么线段AB的长是____．(用含字母m的代数式表示)
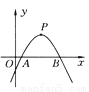
8－2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4，
所以抛物线对称轴所在直线为x=4，交x轴于点D，
所以A.B两点关于对称轴对称，
因为点A(m,0)，且m<4，即AD=4-m，
所以AB=2AD=2(4-m)=8-2m，
故答案为：8-2m.
阅读快车系列答案如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
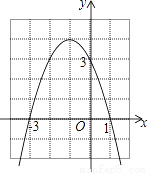
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】试题解析：∵抛物线的顶点坐标为（-1，4），∴二次三项式ax2+bx+c的最大值为4，①正确；
∵x=2时，y＜0，∴4a+2b+c＜0，②正确；
根据抛物线的对称性可知，一元二次方程ax2+bx+c=1的两根之和为-2，③错误；
使y≤3成立的x的取值范围是x≥0或x≤-2，④错误，
故选B． 一列火车从车站开出，预计行程为450千米，当它出发3小时后，因特殊情况而多 停一站，因此耽误30分钟，后来把速度提高了20％，结果准时到达目的地，求这列火车原来的速度.
75千米／时．
【解析】试题分析：设这列火车原来的速度为每小时x千米，则提速后速度为每小时（1+20%）x千米，根据题意可得等量关系：按原速度行驶（450-x）千米所用时间=提速后行驶（450-x）千米所用时间+，列出方程，求解即可．
试题解析：设这列火车原来的速度为x千米／时，根据题意，
得+，
解得x＝75，
经检验x＝75是原方程的解，
所以，这列火车原来... 解分式方程的基本思想是把分式方程化为_________，最后要注意_________．
整式方程 检验
【解析】解分式方程的基本思想是把分式方程化为整式方程，最后要注意检验，
故答案为：整式方程，检验． 已知抛物线y＝ax2+bx+c的大致图象如图所示，试确定a，b，c，b2－4ac及a+b+c的符号．
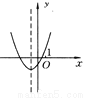
a＋b＋c＞0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析：
∵抛物线开口向上，∴a＞0．∵抛物线与y轴的交点在y轴的负半轴上，∴C＜0．又∵对称轴在y轴左侧，∴ab＞0．∵a＞0，∴b＞0．∵抛物线与x轴有两个交点，∴△＝b2－4ac＞0．∵当x=1时，y＞0，∴a＋b＋c＞... 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（ ）
A. ﹣2 B.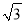 
或-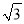
C. 2或-
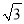D. 2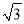或﹣
或-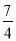
C
【解析】由题意得该抛物线的对称轴为x=m.
①当-2≤m≤1时,此时最大值为,即=4,
解得m= (舍去)或m=-;
②当m>1时,此时当x=1时,函数有最大值,所以,
解得m=2;
③当m<-2时,此时x=-2函数有最大值,所以,
解得m= (不合题意,舍去).
综上所述,m= -或m=2.
所以C选项是正确的. 如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
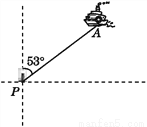
(1)在图中画出点B，并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33,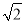 
≈1.41)
（1）点B的位置见解析，PB≈113海里；
（2）灯塔P位于B处的西北(或北偏西45°)方向,距离B处大约113海里.
【解析】试题分析：（1）先在图中画出点B，作PC⊥AB于C，先解Rt△PAC，得出PC=PA•sin∠PAC=80，再解Rt△PBC，得出PB=PC=1.41×80≈113；
（2）由∠CBP=45°，PB≈113海里，即可得到灯塔P位于B处北偏西45°方向，且... 如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）
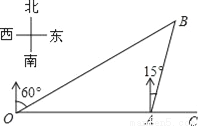
A. 4km B. 2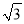
km C. 2
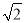km D. （
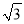+1）km
C
【解析】试题分析：过点A作AD⊥OB，则AD=OA=2km，根据题意可得：△ABD为等腰直角三角形，则AB=2km. 用下列一种正多边形可以拼地板的是（ ）
A． 正五边形 B． 正六边形 C． 正八边形 D． 正十二边形
B
【解析】
试题分析：先计算各正多边形每一个内角的度数，判断是否为360°的约数．
【解析】
A、正五边形的每一个内角度数为180°﹣360°÷5=108°，108°不是360°的约数，故一种正五边形不能拼地板；
B、正六边形的每一个内角度数为180°﹣360°÷6=120°，120°是360°的约数，故一种六边形能拼地板；
C、正八边形的每一个内角度数为180°...