把一个多项式化成几个________的_______的形式，叫做把这个多项式分解因式.
整式 积
【解析】根据因式分解的定义可得：把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式. (x+3)2=x2+6x+9从左到右的变形是_________________.
整式乘法
【解析】根据完全平方公式计算出(x+3)2的结果，属于整式的乘法. 4x2-9=(2x+3)(2x-3)从左到右的变形是__________________.
因式分解
【解析】因式分解是把一个多项式化为几个整式积的形式，由此可得该变形属于因式分解. 计算（1）～（3）题，并根据计算结果将（4）～（6）题进行分解因式.
（1）（x-2）（x-1）＝______； （2）3x（x-2）＝______；
（3）（x-2）2＝______； （4）3x2-6x＝______；
（5）x2-4x+4＝______； （6）x2-3x+2＝______.
x2-3x+2 3x2-6x x2-4x+4 3x(x-2) (x-2)2 (x-2)(x-1)
【解析】（1）根据多项式乘以多项式的乘法法则可得（x-2）（x-1）＝x2-3x+2；（2）根据单项式乘以多项式的乘法法则可得3x（x-2）＝3x2-6x；（3）根据完全平方公式可得（x-2）2＝x2-4x+4；（4）提取公因式3x可得3x2-6x＝3x(x-2)；（5）根据完全平方公式因式分解... 下列由左到右的变形中，哪些是分解因式?哪些不是?请说出理由.
（1）a（x+y）=ax+ay；
（2）x2+2xy+y2-1＝x（x+2y）+（y +1）（y-1）；
（3）ax2-9a＝a（x+3）（x-3）；
（4）x2+2+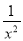
=
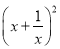
（5）2a3＝2a·a·a.
见解析
【解析】试题分析：根据因式分解的定义判断即可.
试题解析：
因为(1) (2)的右边都不是整式的积的形式.所以它们不是分解因式；(4)中， 都不是整式，(5)中的2a3不是多项式，所以它们也不是分解因式．只有(3)的左边是多项式，右边是整式的积的形式，所以(3)是分解因式. 若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
所以m=-1,n=-2. 已知x2-2x-3=0，则代数式6-2x2+4x的值是多少？
0.
【解析】试题分析：已知x2-2x-3=0，可得x2-2x=3，把代数式6-2x2+4x化为6-2（x2-2x），代入求值即可.
试题解析：
∵x2-2x-3=0，
∴x2-2x=3，
∴6-2x2+4x=6-2（x2-2x）=6-2×3=0. 把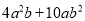
分解因式时，应提取的公因式是____________.
2ab
【解析】把分解因式时，应提取的公因式是2ab. 多项式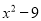
与
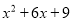的公因式是
x＋3
【解析】分别将多项式ax2-4a与多项式x2-4x+4进行因式分解，再寻找他们的公因式．
【解析】
∵x2-9=（x-3）(x+3)，
x2+6x+9=（x+3）2，
∴多项式x2-9与多项式x2+6x+9的公因式是x+3． 分解因式：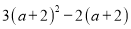 
=______________.
(a+2)(3a+4)
【解析】提取公因式a+2即可，即原式=（a+2）（3a+6-2）=(a+2)(3a+4).