题目内容
4x2-9=(2x+3)(2x-3)从左到右的变形是__________________.
因式分解
【解析】因式分解是把一个多项式化为几个整式积的形式，由此可得该变形属于因式分解.
若二次函数y＝x2＋bx＋4配方后为y＝(x－2)2＋k，则b、k的值分别为( )
A. 0，5 B. 0，1 C. －4，5 D. －4，0
D
【解析】∵二次函数y＝x2＋bx＋4配方后是y＝（x－2）2＋k
∴a=1， -=2， c=4
∴b=-4
∴ k==1
故选：D. 对于抛物线y＝ax2，下列说法中正确的是（ ）
A. a越大，抛物线开口越大
B. a越小，抛物线开口越大
C. ｜a｜越大，抛物线开口越大
D. ｜a｜越小，抛物线开口越大
D
【解析】试题分析：∵对于y＝ax2图像而言，|a|越小，开口越大
∴D是正确的 把多项式（3a－4b）（7a－8b）＋（11a－12b）（8b－7a）分解因式的结果（ ）
A. 8（7a－8b）（a－b） B. 2（7a－8b）2
C. 8（7a－8b）（b－a） D. －2（7a－8b）
C
【解析】把(3a-4b)(7a-8b)+(11a-12b)(8b-7a)运用提取公因式法因式分解即可得(3a-4b)(7a-8b)+(11a-12b)(8b-7a)
=(7a-8b)(3a-4b-11a+12b)
=(7a-8b)(-8a+8b)
=8(7a-8b)(b-a).
故选：C. 把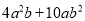
分解因式时，应提取的公因式是____________.
2ab
【解析】把分解因式时，应提取的公因式是2ab. 把多项式(m+1)（m-1）+（m-1）分解因式，一个因式是（m-1）,则另一个因式是（ ）
A. m+1 B. 2m C. 2 D. m+2
D
【解析】∵(m+1)（m-1）+（m-1）=（m-1）（m+1+1）=（m-1）（m+2），
∴另一个因式是（m+2）.
故选D. 如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）探究下列问题：
①若一个函数的特征数为[2，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[4，2]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[2，4]？
（1）此函数图象的顶点坐标为：（1，0）；（2）图象对应的函数的特征数为：[0，﹣1]；（3）原函数的图象向右平移1个单位，再向上平移5个单位得到．
【解析】试题分析：（1）根据特征数的定义，得二次函数为y=x2﹣2x+1，再利用配方得：y=（x﹣1）2，从而顶点坐标为（1,0）
（2）①根据特征数的定义，得二次函数为y=x2+2x-1，再利用配方得y=（x+1）2﹣2，图象先向右平移... 已知抛物线y=ax2+bx+c开口向下，顶点坐标（3，-5），那么该抛物线有（ ）
A. 最小值-5
B. 最大值-5
C. 最小值3
D. 最大值3
B
【解析】由抛物线的开口向下和其顶点坐标为（3，-5），根据抛物线的性质，可以知该抛物线有最大值-5．
故选：B． 若所求的二次函数图象与抛物线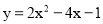
有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（ ）
A.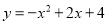 
B.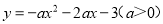 
C.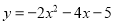 
D.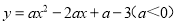 
D
【解析】抛物线y=2x2-4x-1的顶点坐标为（1，-3），根据题意得所求的二次函数的解析式的顶点坐标是（1，-3），且抛物线开口向下．
A．抛物线开口向下，顶点坐标是（1，5），所以选项错误；
B．抛物线开口向下，顶点坐标是（1，-3a-3），所以选项错误；
C．抛物线开口向下，顶点坐标是（-1，-3），所以选项错误；
D．抛物线开口向下，顶点坐标是（1，-3）...