题目内容
(x+3)2=x2+6x+9从左到右的变形是_________________.
整式乘法
【解析】根据完全平方公式计算出(x+3)2的结果，属于整式的乘法.
练习册系列答案
相关题目
抛物线y＝2(x－3)2＋1的顶点坐标是( )
A. (3，1) B. (3，－1) C. (－3，1) D. (－3，－1)
A
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y＝2(x－3)2＋1的顶点坐标是（3，1）．
故选：A． 在二次函数①y＝3x2；②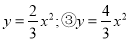
中，图象在同一水平线上的开口大小顺序用题号表示应该为( )
A. ①＞②＞③ B. ①＞③＞②
C. ②＞③＞① D. ②＞①＞③
C
【解析】根据二次函数的性质，可知系数a决定开口方向和开口大小，且a的值越大开口越小，因此可知②＞③＞①.
故选：C. -6xyz+3xy2-9x2y的公因式是（ ）
A. -3x B. 3xz C. 3yz D. -3xy
D
【解析】通过观察可知原式的公因式为-3xy，直接提取即可． 已知x2-2x-3=0，则代数式6-2x2+4x的值是多少？
0.
【解析】试题分析：已知x2-2x-3=0，可得x2-2x=3，把代数式6-2x2+4x化为6-2（x2-2x），代入求值即可.
试题解析：
∵x2-2x-3=0，
∴x2-2x=3，
∴6-2x2+4x=6-2（x2-2x）=6-2×3=0. 下列各式的因式分解中正确的是（ ）
A. -m2+mn-m=-m(m+n-1) B. 9abc-6a2b2=3abc(3-2ab)
C. 3a2x-6bx+3x=3x(a2-2b) D.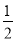 
ab2+
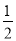a2b=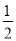
ab(a+b)
D
【解析】选项A，原式=-m(m-n+1)；选项B，原式=3abc(3c-2ab)；选项C，原式=3x(a2-2b+1)；选项D，原式=ab(a+b)；故选D. 把抛物线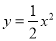
平移得到抛物线m，抛物线m经过点A（-6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线
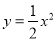交于点Q．
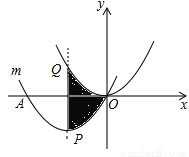
（1）求顶点P的坐标；
（2）写出平移过程；
（3）求图中阴影部分的面积．
（1）（-3， ）；（2）先向左平移3个单位，再向下平移个单位；（3）.
【解析】试题分析：（1）先利用交点式确定平移后的抛物线解析式，然后配成顶点式得到P点坐标；
（2）利用顶点的平移过程得到抛物线的平移过程；
（3）根据平移得到图中阴影部分的面积，然后根据三角形面积公式计算．
试题解析：（1）平移的抛物线解析式为= =，
所以顶点P的坐标为（-3， ）；
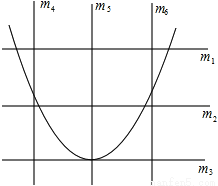
（... 王芳将如图所示的三条水平直线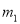
， 
， 
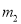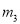的其中一条记为x轴（向右为正方向），三条竖直直线
， 
， 
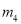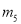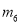的其中一条记为y轴（向上为正方向），并在此坐标平面内画出了抛物线
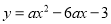，则她所选择的x轴和y轴分别为（ ）
A.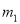 
， 
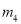
B.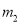 
， 
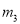
C.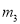 
， 
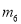
D.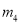 
， 
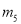
A
【解析】根据抛物线开口向上可知a＞0，将抛物线配方为，可得抛物线的对称轴为x=3，可知应选择的y轴为直线；由顶点坐标为（3，-3-9a），抛物线与y轴的交点为（0，-3），而-3-9a＜-3，可知应选择的x轴为直线，
故选：A． 抛物线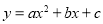
与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线
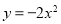相同，则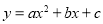的函数关系式为（ ）
A．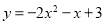
B．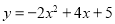
C．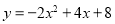
D．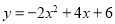
D．
【解析】
试题分析：由题意a=﹣2，∵抛物线与x轴的两个交点为（﹣1，0），（3，0）∴设y=﹣2（x+1）（x﹣3），即：．故选D．