掷一枚正方体的骰子，各个面上分别标有数字1， 2，3，4，5，6，求下列事件发生的频率的大小：
①朝上的数字是奇数；
②朝上的数字能被3除余1；
③朝上的数字不是3的倍数；
④朝上的数字小于6；
⑤朝上的数字不小于3.
①；②；③；④；⑤
【解析】试题分析:本题考察可能性大小的应用，关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，每一个点数出现的频率相同.其中，是奇数点的有3种可能，故其频率是；
②【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，... 从一副扑克牌中任取一张，则抽到红桃的频率与抽到黑桃的频率哪个大？抽到梅花与抽到大、小王的频率哪个大？
抽到红桃的可能性与抽到黑桃的频率一样大，而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用，关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，抽到红桃的的频率为，抽到黑桃的的频率为，抽到梅花的的频率为，抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到... 如图是若干张卡片，它们的背面都一样，现将它们背面朝上，从中任意摸一张卡片，摸到几号卡片的频率大？
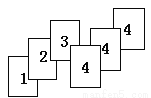
摸到4号卡片的频率大.
【解析】试题分析: 本题考察可能性大小的应用，根据不同编号卡片的数量求出不同编号卡片被抽到的概率是解答本题的关键.
解答：因为给出的六张卡片中，1号卡片有1张，2号有1张，3号有1张，4号有3张.所以摸到1号卡片的频率为，摸到2号卡片的频率为，摸到3号卡片的频率为，摸到4号卡片的频率为.所以，摸到4号卡片的频率大. 我会连.（任意摸出一个球，可能是什么颜色？）
一定是白球 可能是白球 不可能是白球
【解析】试题分析: 本题考察对可能性大小的应用，关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的，第一个袋子中全是黑球，第二是全是白球，第三个里面有黑球也有白球，所以，从第二个袋子中摸出的一定是白球，第一个袋子中摸出来的一定不是白球；第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示. 掷一枚质地均匀的骰子，看落地后朝上的面的点数.
（1）会出现哪些可能的结果？
（2）掷出的点数为1与掷出的点数为2的频率相同吗？掷出的点数为1与掷出的点数为3的频率相同吗？
（3）每种结果出现的频率相同吗？
（1）可能出现朝上的面的点数是：1，2，3，4，5，6；（2）掷出的点数为1与掷出的点数为2的频率相同；掷出的点数为1与掷出的点数为3的频率相同；（3）每种结果出现的频率相同
【解析】试题分析: 掷一个质地均匀的骰子，有6种等可能的结果，每个数字的频率都稳定在 ，所以每种结果出现的可能性都相同.
（1）【解析】
掷一枚质地均匀的骰子，由于有六个面，所以落地后，可能出现朝上的面的点数是... 已知?ABCD的周长为32，AB=4，则BC=（ ）
A. 4 B. 12 C. 24 D. 28
B
【解析】【解析】
由题意得，，AB=4，解得BC=12，故选B。 在平行四边形ABCD中，∠B＝60°，那么下列各式中，不能成立的是( )
A．∠D＝60°
B．∠A＝120°
C．∠C＋∠D＝180°
D．∠C＋∠A＝180°
D
【解析】∵四边形ABCD是平行四边形，∴∠D＝∠B＝60°．故A正确；∵AD∥BC，∴∠C＋∠D＝180°，故C正确；∵AD∥BC，∴∠A＋∠B＝180°，∴∠A＝180°－∠B＝120°，故B正确；∵四边形ABCD是平行四边形，∴∠C＝∠A＝120°，故D不正确，故选D． 如图，在平行四边形ABCD中，AB＞BC，按以下步骤作图：以A为圆心，小于AD的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于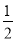
EF的长半径画弧，两弧交于点G；作射线AG交CD于点H．则下列结论：①AG平分∠DAB，②CH=
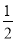DH，③△ADH是等腰三角形，④S△ADH=
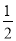S四边形ABCH．
其中正确的有（ ）
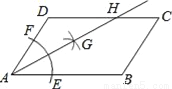
A. ①②③ B. ①③④ C. ②④ D. ①③
D
【解析】试题分析：①如图，连接EG，FG，
由作图可得，AE=AF，EG=FG，
又∵AG=AG，∴△AEG≌△AFG（SSS）。
∴∠EAG=∠FAG，即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中，DC∥AB，∴∠HAB=DHA。
由①∠HAB=∠HAD，∴∠HAD=DHA。∴DA=DH，即△ADH是等腰三角形。故结论③正确。
②若... 在△MNB中，BN=6，点A，C，D分别在MB，NB，MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是（ ）
A．24 B．18 C．16 D．12
D
【解析】
在平行四边形ABCD中CD∥AB，AD∥BC，∴∠M=∠NDC，∠N=∠MDA，∵∠NDC=
∠MDA，∴∠M=∠N=∠NDC=∠MDA，∴MB=BN=6，CD=CN，AD=MA，∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12． 如图，在平行四边形ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是：①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边△；④CG⊥AE（ ）
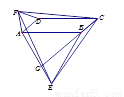
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
B
【解析】根据题意，结合图形，对选项一一求证，判定正确选项
【解析】
在□ABCD中，∠ADC=∠ABC，AD=BC，CD=AB，
∵△ABE、△ADF都是等边三角形，
∴AD=DF，AB=EB，∠ADF=∠ABE=60°，
∴DF=BC，CD=BC，
∴∠CDF=360°-∠ADC-60°=300°-∠ADC，
∠EBC=360°-∠ABC-60°=300°-∠ABC，...