题目内容
在平行四边形ABCD中，∠B＝60°，那么下列各式中，不能成立的是( )
A．∠D＝60°
B．∠A＝120°
C．∠C＋∠D＝180°
D．∠C＋∠A＝180°
D
【解析】∵四边形ABCD是平行四边形，∴∠D＝∠B＝60°．故A正确；∵AD∥BC，∴∠C＋∠D＝180°，故C正确；∵AD∥BC，∴∠A＋∠B＝180°，∴∠A＝180°－∠B＝120°，故B正确；∵四边形ABCD是平行四边形，∴∠C＝∠A＝120°，故D不正确，故选D．
练习册系列答案
相关题目
一个多边形的内角度数从小到大排列起来，恰好依次增加相同的度数，其中最小角是
，最大角是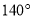
,求这个多边形的边数.
6
【解析】本题考查的是多边形的性质
根据“依次增加相同的度数，其中最小角是，最大角是”即可解得结果，注意边数为正整数。
设多边形的边数是，依次增加，
则
解得符合题意的正整数解
答：这个多边形的边数为 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A. 频率就是概率
B. 频率与试验次数无关
C. 概率是随机的,与频率无关
D. 随着试验次数的增加,频率一般会越来越接近概率
D
【解析】因为大量重复试验事件发生的频率逐渐稳定到某个常数附近，可以用这个常数估计这个事件发生的概率,所以D选项说法正确,故选D. 满足下列条件的三角形不一定是直角三角形的是（ ）
A. 三条边的比为5：12：13
B. 三个角的度数比为2：3：5
C. 有一边等于另一条边的一半
D. 三角形的三边长分别是24、25和7
C
【解析】A、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
B、因为根据三角形内角和定理可求出三个角分别为36度，54度，90度，所以是直角三角形，故正确；
C、因为根据三角形内角和公式得三个角中没有90°角，所以不是直角三角形，故不正确；
D、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
故选C． 如图，平行四边形ABCD中，AC=4cm，BC=5cm，CD=3cm，则?ABCD的面积__．
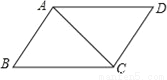
12cm2
【解析】 ∵四边形ABCD是平行四边形，
∴AB=CD=3cm，
∵AC=4cm，BC=5cm，
∴AC2+AB2=AC2，
∴△ABC是直角三角形，
∴S△ABC=×3×4=6cm2，
∴则ABCD的面积=2×6=12cm2. 从一副扑克牌中任取一张，则抽到红桃的频率与抽到黑桃的频率哪个大？抽到梅花与抽到大、小王的频率哪个大？
抽到红桃的可能性与抽到黑桃的频率一样大，而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用，关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，抽到红桃的的频率为，抽到黑桃的的频率为，抽到梅花的的频率为，抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到... 从一副扑克牌中则下列事件中可能性最大的是( )
A. 抽出一张红心 B. 抽出一张红色老K C. 抽出一张梅花J D. 抽出一张不是Q的牌
D
【解析】一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，任意抽出一张，抽到红桃的概率为，抽到黑桃的概率为，抽到梅花的概率为，抽到大、小王的概率为，抽出一张不是Q牌的概率为，对照这些数据，可以得到可能性最大的是D.
故选D. 已知?ABCD的周长为36cm，过点A作AE⊥BC，AF⊥CD，垂足分别为E、F.若AE＝2cm，AF＝4cm.求?ABCD的各边长．
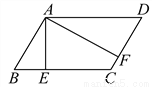
AB＝CD＝6cm，AD＝BC＝12cm.
【解析】【试题分析】根据?ABCD的周长为36cm，得BC＋CD＝18；根据等面积法，得S?ABCD＝BC·AE＝CD·AF，解得：BC＝2CD，两式联立方程组，，解得，根据平行四边形的对边相等，得AB＝CD＝6cm，AD＝BC＝12cm.
【试题解析】
∵?ABCD中，AB＝CD，BC＝AD，又∵?ABCD的周长为36cm.即AB＋B... △ABC和△AˊBˊCˊ关于点O对称，下列结论不正确的是（ ）
A. AO=AˊO
B. AB∥AˊBˊ
C. CO=BO
D. ∠BAC=∠BˊAˊCˊ
C
【解析】因为只有对称点到对称中心的距离相等，所以C选项是错误的
故选C.