题目内容
如图，在平行四边形ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是：①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边△；④CG⊥AE（ ）
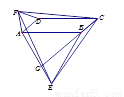
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
B
【解析】根据题意，结合图形，对选项一一求证，判定正确选项
【解析】
在□ABCD中，∠ADC=∠ABC，AD=BC，CD=AB，
∵△ABE、△ADF都是等边三角形，
∴AD=DF，AB=EB，∠ADF=∠ABE=60°，
∴DF=BC，CD=BC，
∴∠CDF=360°-∠ADC-60°=300°-∠ADC，
∠EBC=360°-∠ABC-60°=300°-∠ABC，...
期末1卷素质教育评估卷系列答案已知和多边形一个内角相邻的外角与其余各内角度数总和为600°，求该多边形的边数．
边数为5或6．
【解析】分析：设多边形的边数为n,内角为x,根据多边形内角和定理得到(n－2)×180°－x＋180－x＝600，化简用含n的式子表示x,再由0＜x＜180，得到n的取值范围，结合n为正整数即可求解.
本题解析：
设边数为n，这个内角的度数为x.根据题意，得
(n－2)×180°－x＋180－x＝600.
解方程，得x＝90n－390.
∵ 0＜... 林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的 棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的 棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的 频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为_________.
0.88
【解析】因为（0.865+0.904+0.888+0.875+0.882+0.878+0.879+0.881）÷8≈0.88,所以这种幼树移植成活率的概率约为0.88,故答案为:0.88. 如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（ ）
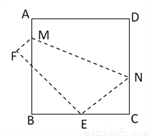
A. 3cm B. 4cm C. 5cm D. 6cm
A
【解析】分析：根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8-x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．
解答：【解析】
设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8-x）2=16+x... 如图所示，在?ABCD中，E为AD中点，CE交BA的延长线于F，若BC=2AB，∠FBC=70°，则∠EBC的度数为__度．
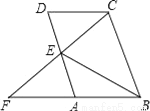
35
【解析】∵ABCD，
∴AB=CD，DC∥AB，
∴∠ECD=∠EFA,
∵DE=AE，∠DEC=∠AEF,
∴△DEC≌△AEF,
∴DC=AF,
∴AB=AF.
∵BC=2AB，AB=AF,
∴BC=BF,
∴△FBC为等腰三角形,
再由△DEC≌△AEF，得EC=EF,
∴∠EBC=∠EBF=∠CBF=×70°=3... 掷一枚质地均匀的骰子，看落地后朝上的面的点数.
（1）会出现哪些可能的结果？
（2）掷出的点数为1与掷出的点数为2的频率相同吗？掷出的点数为1与掷出的点数为3的频率相同吗？
（3）每种结果出现的频率相同吗？
（1）可能出现朝上的面的点数是：1，2，3，4，5，6；（2）掷出的点数为1与掷出的点数为2的频率相同；掷出的点数为1与掷出的点数为3的频率相同；（3）每种结果出现的频率相同
【解析】试题分析: 掷一个质地均匀的骰子，有6种等可能的结果，每个数字的频率都稳定在 ，所以每种结果出现的可能性都相同.
（1）【解析】
掷一枚质地均匀的骰子，由于有六个面，所以落地后，可能出现朝上的面的点数是... 一个口袋中装有5个红球，3个白球，1个绿球，摸到白球的频率______摸到绿球的频率(填“大于”“小于”或“等于”)
大于
【解析】由题意知这个口袋中装有5个红球，3个白球，1个绿球，共有5+3+1=9个球，摸到红球的概率是，摸到白球的概率是，摸到红球的概率是，因此，摸到白球的概率大于摸到绿球的概率. 某单位要在两名射击队员中推出一名参加比赛，已知同等条件下，甲射中某物的可能性大于乙，则所推出的人中应（ ）
A. 选甲 B. 选乙 C. 都可以 D. 不能确定
A
【解析】根据题意可知，同等条件下，甲射中某物的可能性大于乙.故应该派甲去.
故选A. 在下列图形中，是中心对称图形的是( )
A. 
B. 
C. 
D. 
C
【解析】试题分析：A、旋转180°后不能与自身重合，不是中心对称图形；
B、旋转180°后不能与自身重合，不是中心对称图形；
C、旋转180°后能与自身重合，是中心对称图形；
D、旋转180°后不能与自身重合，不是中心对称图形．
故选C．