题目内容
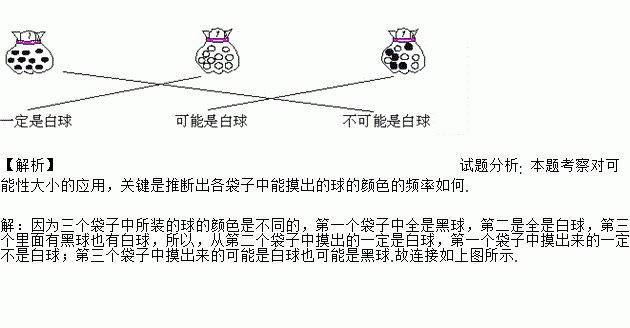
我会连.(任意摸出一个球,可能是什么颜色?)



一定是白球 可能是白球 不可能是白球
 【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示.
【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示.
练习册系列答案
相关题目
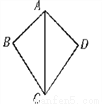
如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
 2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2.
2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2. 某收费站在2 h内对经过该站的机动车统计如下表:
类型 | 轿车 | 货车 | 客车 | 其他 |
数量/辆 | 36 | 24 | 8 | 12 |
若有一辆机动车经过这个收费站,利用上面的统计表估计它是轿车的概率为( )
A.  B.
B. 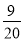 C.
C. 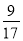 D.
D. 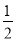
 B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B.
B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B. 如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
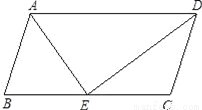
 (1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中...
(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中... 在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则四边形ABCD的周长是( )

A.24 B.18 C.16 D.12
 D
【解析】
在平行四边形ABCD中CD∥AB,AD∥BC,∴∠M=∠NDC,∠N=∠MDA,∵∠NDC=
∠MDA,∴∠M=∠N=∠NDC=∠MDA,∴MB=BN=6,CD=CN,AD=MA,∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12.
D
【解析】
在平行四边形ABCD中CD∥AB,AD∥BC,∴∠M=∠NDC,∠N=∠MDA,∵∠NDC=
∠MDA,∴∠M=∠N=∠NDC=∠MDA,∴MB=BN=6,CD=CN,AD=MA,∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12. 目前,我国农村人口A与非农村人口B的比例如图所示,当转盘停止转动时,指针停在_______区域的可能性较大.

 A
【解析】试题分析:通过比较,看A、B两部分哪一部分在转盘中所占的面积大,哪部分面积大说明指针停在哪一部分的可能性大.
由图可知:A部分占的比例比B部分占的比例大,
所以当转盘停止转动时,指针停在A区域的可能性较大.
A
【解析】试题分析:通过比较,看A、B两部分哪一部分在转盘中所占的面积大,哪部分面积大说明指针停在哪一部分的可能性大.
由图可知:A部分占的比例比B部分占的比例大,
所以当转盘停止转动时,指针停在A区域的可能性较大. “任意买一张电影票,座位号是2的倍数”,此事件是( )
A. 不可能事件 B. 不确定事件 C. 必然事件 D. 以上都不是
 B
【解析】试题分析:因为电影票的座位号可能是奇数,也可能是偶数,所以任意买一张电影票,座位号是2的倍数,可能发生也可能不发生,所以此事件是不确定事件,故选:B.
B
【解析】试题分析:因为电影票的座位号可能是奇数,也可能是偶数,所以任意买一张电影票,座位号是2的倍数,可能发生也可能不发生,所以此事件是不确定事件,故选:B. 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为__.
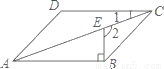
 110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°.
110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°. 下列图形中是轴对称而不是中心对称图形的是( )
A. 平行四边形
B. 线段
C. 角
D. 正方形
 C
【解析】试题解析:平行四边形的对称中心为两条对角线的交点,不是轴对称图形;线段的对称中心为线段的中点,对称轴为线段的中垂线;角不是中心对称图形,对称轴为角平分线所在直线;正方形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线及两条对边中点连线所在直线;所以选择C.
C
【解析】试题解析:平行四边形的对称中心为两条对角线的交点,不是轴对称图形;线段的对称中心为线段的中点,对称轴为线段的中垂线;角不是中心对称图形,对称轴为角平分线所在直线;正方形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线及两条对边中点连线所在直线;所以选择C.