题目内容
掷一枚正方体的骰子，各个面上分别标有数字1， 2，3，4，5，6，求下列事件发生的频率的大小：
①朝上的数字是奇数；
②朝上的数字能被3除余1；
③朝上的数字不是3的倍数；
④朝上的数字小于6；
⑤朝上的数字不小于3.
①；②；③；④；⑤
【解析】试题分析:本题考察可能性大小的应用，关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，每一个点数出现的频率相同.其中，是奇数点的有3种可能，故其频率是；
②【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，...
云南师大附小一线名师提优作业系列答案若一个三角形的三边长分别为3 m，4 m，5 m，那么这个三角形的面积为___.
6 m2
【解析】根据勾股定理的逆定理，可由三边的长判断出此三角形是直角三角形，3cm、4cm是三角形的两直角边，所以根据三角形的面积公式可得面积为3×4÷2=6m2.
故答案为：6m2. 在△ABC中，BC=a，AC=b，AB=c，设c为最长边，当a2+b2=c2时，△ABC是直角三角形；当a2+b2≠c2时，利用代数式a2+b2和c2的大小关系，探究△ABC的形状（按角分类）．
（1）当△ABC三边分别为6、8、9时，△ABC为 三角形；当△ABC三边分别为6、8、11时，△ABC为 三角形．
（2）猜想，当a2+b2 c2时，△ABC为锐角三角形；当a2+b2 c2时，△ABC为钝角三角形．
（3）判断当a=2，b=4时，△ABC的形状，并求出对应的c的取值范围．
【解析】
（1）锐角；钝角。
（2）＞；＜。
（3）①当4≤c＜2时，这个三角形是锐角三角形；
②当c=2时，这个三角形是直角三角形；
③当2＜c＜6时，这个三角形是钝角三角形．。
【解析】
试题分析：（1）利用勾股定理列式求出两直角边为6、8时的斜边的值，然后作出判断即可：
∵两直角边分别为6、8时，斜边=10，
∴当△ABC三边分别为6、8、9... 如图，□ABCD与□DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为_______°．
【解析】∵□ABCD与□DCFE的周长相等，且有公共边CD，
∴AD＝DE，∠ADE＝∠BCF＝60°＋70°＝130°．
∴． 已知?ABCD的周长为32，AB=4，则BC=（ ）
A. 4 B. 12 C. 24 D. 28
B
【解析】【解析】
由题意得，，AB=4，解得BC=12，故选B。 如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是_______.
【解析】试题解析：∵两个同心圆被等分成八等份，飞镖落在每一个区域的机会是均等的，其中白色区域的面积占了其中的四等份，
∴P（飞镖落在白色区域）=. 口袋中有9个球，其中4个红球，3个蓝球，2个白球，在下列事件中，发生的可能性为1的是（ ）
A. 从口袋中拿一个球恰为红球 B. 从口袋中拿出2个球都是白球
C. 拿出6个球中至少有一个球是红球 D. 从口袋中拿出的5个球恰为3红2白
C
【解析】对于A，从口袋中拿一个球恰为红球，可能性小于1,故不符合题意；
对于B，从口袋中拿出2个球都是白球，这是一个随机事件，发生的可能性小于1,故不符合题意；
对于C，拿出6个球中，至少有一个球是红球是正确的，因为蓝球3个，白球5个，如果在极端情况下，这6个球尽可能的不是红球，那么最多有五个不是红球，至少有一个是红球，所以C正确.
对于D, 从口袋中拿出的5个球恰为3... 已知，在?ABCD中，BC-AB=2cm，BC=4cm，则?ABCD的周长是（ ）
A．6cm B．12cm C．8cm D．10cm
B.
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，BC=AD，
∵BC-AB=2cm，BC=4cm，
∴AB=DC=2cm，
∴?ABCD的周长是=2+2+4+4=12cm．
故选B． 如果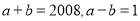
，那么
=___________.
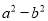2008
【解析】试题解析：∵a2-b2=（a+b）（a-b），
∴把a+b=2008，a-b=1代入上式得：
原式=2008×1=2008．
故答案为：2008．