已知平行四边形ABCD中，∠B=4∠A，则∠C=__．
36°
【解析】试题解析：∵四边形BCDA是平行四边形，
∴AD∥CB，∠A=∠C，
∴∠A+∠B=180°，
∵∠B=4∠A，
∴∠A+4∠A=180°，
解得：∠A=36°，
∴∠C=36°. 如图，平行四边形ABCD中，AC=4cm，BC=5cm，CD=3cm，则?ABCD的面积__．
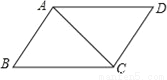
12cm2
【解析】 ∵四边形ABCD是平行四边形，
∴AB=CD=3cm，
∵AC=4cm，BC=5cm，
∴AC2+AB2=AC2，
∴△ABC是直角三角形，
∴S△ABC=×3×4=6cm2，
∴则ABCD的面积=2×6=12cm2. 如图，□ABCD与□DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为_______°．
【解析】∵□ABCD与□DCFE的周长相等，且有公共边CD，
∴AD＝DE，∠ADE＝∠BCF＝60°＋70°＝130°．
∴． 如图，△ACE是以平行四边形ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，CE交x轴于点H．若E点的坐标是(7，一3
)，则D点的坐标是__________．
(5，0)
【解析】试题分析：如图，设EC与x轴交于点Q,由点C与点E关于x轴对称可得出（7，3），CE=6，因△ACE是以□ABCD的对角线AC为边的等边三角形，所以AC=CE=6，根据勾股定理即可求出AQ的长为9，又因OQ=7，所以OA=DQ=2，再求得OD=5，即可得D点的坐标是（5,0）． 如图所示，在?ABCD中，E为AD中点，CE交BA的延长线于F，若BC=2AB，∠FBC=70°，则∠EBC的度数为__度．
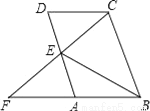
35
【解析】∵ABCD，
∴AB=CD，DC∥AB，
∴∠ECD=∠EFA,
∵DE=AE，∠DEC=∠AEF,
∴△DEC≌△AEF,
∴DC=AF,
∴AB=AF.
∵BC=2AB，AB=AF,
∴BC=BF,
∴△FBC为等腰三角形,
再由△DEC≌△AEF，得EC=EF,
∴∠EBC=∠EBF=∠CBF=×70°=3... 如图，已知平行四边形ABCD，DE是∠ADC的角平分线，交BC于点E．
（1）求证：CD=CE；
（2）若BE=CE，∠B=80°，求∠DAE的度数．
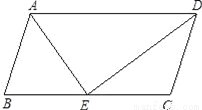
（1）证明见解析；（2）∠DAE=50°．
【解析】试题分析:（1）根据DE是∠ADC的角平分线得到∠1=∠2，再根据平行四边形的性质得到∠1=∠3，所以∠2=∠3，根据等角对等边即可得证；
（2）先根据BE=CE结合CD=CE得到△ABE是等腰三角形，求出∠BAE的度数，再根据平行四边形邻角互补得到∠BAD=100°，所以∠DAE可求．
（1）证明：如图，在平行四边形ABCD中... 已知：如图，在?ABCD中，∠ADC，∠DAB的平分线DF，AE分别与线段BC相交于点F，E，DF与AE相交于点G．
（1）求证：AE⊥DF；
（2）若AD＝10，AB＝6，AE＝4，求DF的长．
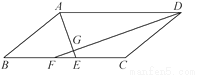
（1）证明见解析；（2）．
【解析】试题分析：（1）根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°，根据角平分线得到∠ADF+∠DAE=（∠ADC+∠DAB）=90°，即可求出结论；
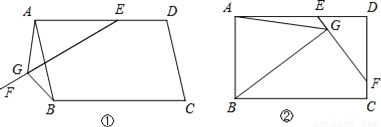
（2）过点D作DH∥AE，交BC的延长线于点H，得到平行四边形AEHD，求出DH=AE=4，EH=AD=10，根据平行四边形的性质和平行线的性质推出DC=FC，AB=EB，求出BF、F... 在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
（1）证明见解析；（2）EG=AG﹣BG，理由见解析．
【解析】试题分析：（1）如图，作∠GAH=∠EAB交GE于点H，易证△ABG≌△AEH ，再判定△AGH是等边三角形，即可得结论；（2）EG=AG-BG，如图②，作∠GAH=∠EAB交GE于点H，类比（1）的方法证明△ABG≌△AEH，再判定△AGH是等腰直角三角形，即可得结论.
试题解析：
如图，作∠GAH=∠EAB交GE... 满足下列条件的三角形不一定是直角三角形的是（ ）
A. 三条边的比为5：12：13
B. 三个角的度数比为2：3：5
C. 有一边等于另一条边的一半
D. 三角形的三边长分别是24、25和7
C
【解析】A、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
B、因为根据三角形内角和定理可求出三个角分别为36度，54度，90度，所以是直角三角形，故正确；
C、因为根据三角形内角和公式得三个角中没有90°角，所以不是直角三角形，故不正确；
D、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
故选C． 已知下列命题：
①若a≤0，则|a|=﹣a；
②若ma2＞na2，则m＞n；
③两组对角分别相等的四边形是平行四边形；
④垂直于弦的直径平分弦．
其中原命题与逆命题均为真命题的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①若a≤0，则|a|=﹣a是真命题，逆命题为若|a|=﹣a，则a≤0是真命题，
②若ma2＞na2，则m＞n是真命题，逆命题为若m＞n，则ma2＞na2是假命题，
③两组对角分别相等的四边形是平行四边形是真命题，逆命题为平行四边形的两组对角分别相等是真命题，
④垂直于弦的直径平分弦是真命题，逆命题为平分弦的直径垂直于弦是假命题，
所以原命题与逆命题均为真命...